Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Green

Ver Teoria
Exercício 161234567891011121314151718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UTFPR. Campus Pato Branco. Cálculo 3. Prova AV2. 2021.2. Questão 1.

Questão 1. Calcule ∫ C F d γ , onde F x , y = ( x 2 - 3 y ) i + sin ⁡ y 4 + y 3 j e a curva C consiste no segmento de reta de 0 ,   - 1 a 1,0 , no arco de circunferência x 2 + y 2 = 1 ; x , y ≥ 0 de 1,0 a 0,1 e no segmento de reta de 0,1 a 0 , - 1 .

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão temos que obter a integral ∫ C F d γ onde C é a região limitada pelo segmento de reta que passa pelos pontos 0 ,   - 1 e 1,0 , no arco de circunferência x 2 + y 2 = 1 em que x e y são maiores que 0 e que passam de 1,0 a 0,1 e no seguimento de reta que passa pelos pontos 0,1 e 0 , - 1 .

Tem ideia do que podemos fazer para obter o resultado dessa integral? 🤔🤔

Primeiro de tudo, temos que obter a região de integração C . Esboçando os pontos, os seguimentos e o arco x 2 + y 2 = 1 contido entre 1,0 e 0,1 , temos

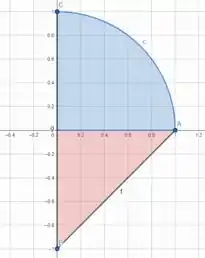
Perceba que a região C é fechada e como F é uma função vetorial dada por

F x , y = x 2 - 3 y i + sin ⁡ y 4 + y 3 j

Podemos aplicar o Teorema de Green.

Bora ver como fazemos isso? 😉😉

Passo 2

O Teorema de Green nos diz que podemos reescrever uma integral de linha em uma região fechada como

∫ C F d γ = ∬ A Q x - P y d A

Se a função F é, genericamente, dada por F x , y = P x , y i + Q x , y j . Se compararmos com a função dada, vemos que P x , y = x 2 - 3 y e Q x , y = sin ⁡ y 4 + y 3 .

Derivando Q com relação a x , temos

∂ Q ∂ x = ∂ sin ⁡ y 4 + y 3 ∂ x

Como não temos x para derivar, então é como se estivéssemos derivando uma constante, sabemos que a derivada de uma constante é 0 , então...

∂ Q ∂ x = 0

Agora derivando P com relação a y , temos

∂ P ∂ y = ∂ x 2 - 3 y ∂ y

Derivando pelo método de derivação polinomial, lembrando que para ∂ y , x é uma constante...

∂ P ∂ y = x 2 0 - 3 y 1 - 1

∂ P ∂ y = - 3

Substituindo no Teorema de Green, temos

∫ C F d γ = ∬ A Q x - P y d A

∫ C F d γ = ∬ A 0 - - 3 d A

∫ C F d γ = ∬ A 3 d A

Tranquilo até aqui? 😁

Passo 3

Vamos dar uma analisada na integral ∬ A 3 d A

Como 3 é uma constante, podemos tirá-la da integral...

∫ C F d γ = 3 ∬ A d A

Mas o que é ∬ A d A ?

A integral dupla de uma região nos dá a área dessa região, concorda? 😎

Então, podemos dividir nossa área em duas partes

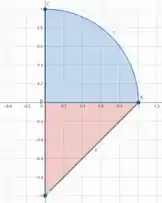
A parte do triangulo vermelho e a parte do setor circular azul!

A área do triangulo é dada por

A 1 = b · h 2

Pela figura, vemos que a base b é 1 e a altura h também é 1 , logo

A 1 = 1 · 1 2 = 1 2

Para a área 2 , perceba que o setor circular que é formado, representa 1 / 4 da área de um círculo, ou seja

A 2 = 1 4 π r 2

Se o raio r é 1 , então

A 2 = 1 4 π 1 2 = π 4

Por fim, temos que

∬ A d A = A 1 + A 2 = 1 2 + π 4

∬ A d A = π + 2 4

Substituindo na equação do Teorema...

∫ C F d γ = 3 ∬ A d A = 3 π + 2 4

∫ C F d γ = 3 π + 6 4

E esse é o valor que encontramos para ∫ C F d γ ! Legal né? 🤩

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

∫ C F d γ = 3 π + 6 4

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x