Questão 5: Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
Onde é a fronteira da região englobada pelas parábolas e .
Passo 1
Bem, antes de começarmos o nosso problema, vamos apenas mudar a notação dessa integral de linha para uma notação mais famosa:
Onde é o campo vetorial dado por:
Queremos resolvê-la por GREEN. Um teorema muito bom que nos ajuda a resolver integrais de linha trocando-a por uma integral dupla muito especial:
Passo 2
Mas agora, antes de aplicar essa igualdade na risca, precisamos antes verificar se estamos nas condições do teorema de forma certinha. Green nos exige três coisas:
- Uma curva fechada delimitando a região .
- Uma orientação positiva.
- Um campo sem singularidades.
Antes então de aplicar o Teorema, nos próximos três passos nos dedicaremos a verificar cada uma dessas exigências. Se elas estiverem ok, o passo 6 é resolvendo então o problema. Vamos nessa?
Passo 3
A primeira exigência trata-se de garantir que a nossa curva fecha uma região . Pelo enunciado sabemos que:
“Onde é a fronteira da região englobada pelas parábolas e .”
Se desenharmos essas parábolas aí...
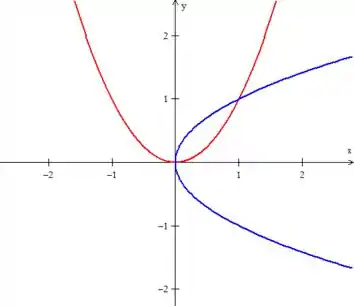
Ganhamos então a curva delimitando a região como pedida no problema:
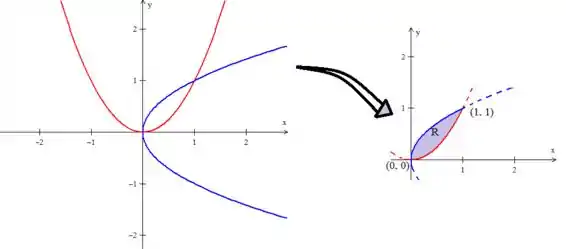
Veja que essas curvas se encontram no ponto e no ponto . Você encontra esses pontos fazendo a intersecção matemática deles:
Passo 4
A curva deve estar orientada positivamente para aplicarmos o Teorema... Isso significa que ela deve estar girando no sentido anti-horário:
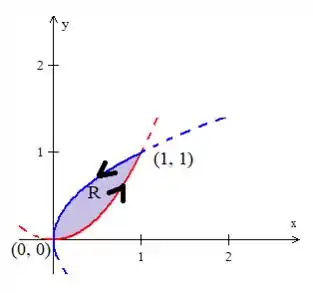
Mas não se preocupe com isso, pois o problema já nos disse que a orientação já é positiva!
Passo 5
Quanto ao último quesito... Ao do campo não possuir singularidades, vejamos:
Veja que esse campo para qualquer valor que tenha , devido a raiz, ele funciona bem. Ele até tem singularidades, mas não é onde estamos trabalhando, pois a nossa curva e a região no seu interior tem o , saca? Então estamos sem problemas aqui também .
Passo 6
Finalmente podemos regressar para a integral de linha:
E pela igualdade de GREEN, a calcula-la através da integral dupla. Bora?
Passo 7
Primeiro, vamos encontrar essa função do integrando...
Como a gente conhece e :
Logo...
Então a integral dupla que temos que integrar é:
Passo 8
Mas calma, JOVEM, quem ainda precisamos descrever a região . Como nossa região é:
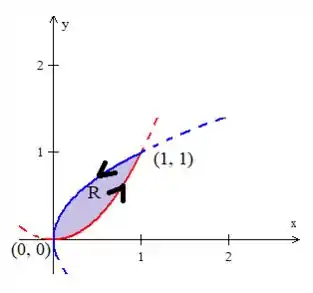
Podemos descrevê-la como se fosse uma região do TIPO 1, onde o varia do primeiro ponto ao último ...
Já o varia da base da parábola em pé, até o teto da parábola deitada...
Como a parábola em pé é e a parábola deitada ...
Passo 9
Com isso em mãos ganhamos...
Calculando...