USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 2 - 2022.1, Questão 10h
Usando o Teorema de Green, calcule as seguintes integrais de linha:
h) , onde e consiste do arco de circunferência de a e dos segmentos de reta de a e de a .
Passo 1
Olá meu amigo, tudo bem? Yuri aqui e agora iremos calcular essa querida integral utilizando o famoso teorema de Green. O teorema de Gree diz o seguinte:
Seja C uma curva plana simples, fechada, contínua por partes, orientada positivamente, e seja D a região delimitada por C. Se P e Q têm derivadas parciais de primeira ordem contínuas sobre uma região aberta que contenha D, então
então vamos aplicar esse teorema para o nosso caso aqui.
Passo 2
Olá meu amigo, então iremos aqui aplicar o teorema de Green. Primeiro vamos aplica-lo a equação e depois iremos descobrir quem é a região dA.
Então agora vamos dar uma olhada no dA
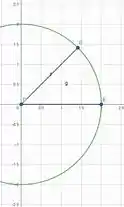
Agora iremos ser inteligentes, eu e voce meu caro colega, e iremos utilizar uma parametrização para trabalhar aqui
O nosso raio é
O que resta é descobrirmos o valor de
Para o ponto
Então
Passo 3
Agora é hora de montar e calcular nossa integral