Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Green

Ver Teoria
Exercício 371234567891011121314151617181920212223242526272829303132333435363839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Teorema de Green

Considere a integral de linha

I = ∮ C F ∙ d r

Onde C é a fronteira da região do primeiro quadrante limitada pelas circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 e F é o campo vetorial definido por F x , y = x x 2 + y 2 , - y x 2 + y 2

Calcule I usando obrigatoriamente o teorema de Green

Passo 1

Temos que usar o teorema de Green, já que ele disse que precisamos né? Rs, aquela integral de linha vai ficar

I = ∮ C F ∙ d r = ∬ D ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Onde D é a região que tem C como fronteira. Como C é fechada e a função F está definida em todo ponto fora a origem, e a origem não está na região D , podemos usar sem preocupação o teorema de Green.

Vamos calcular ∂ F 2 ∂ x - ∂ F 1 ∂ y , começando com as derivadas, usando a regra do quociente

∂ F 2 ∂ x = ∂ ∂ x - y x 2 + y 2 = 0 x 2 + y 2 - 2 x - y x 2 + y 2 2 = 2 x y x 2 + y 2 2

E

∂ F 1 ∂ y = ∂ ∂ y x x 2 + y 2 = 0 x 2 + y 2 - 2 x x x 2 + y 2 2 = - 2 x y x 2 + y 2 2

Vamos ter

∂ F 2 ∂ x - ∂ F 1 ∂ y = 2 x y x 2 + y 2 2 - - 2 x y x 2 + y 2 2 = 2 x y x 2 + y 2 2 + 2 x y x 2 + y 2 2 = 4 x y x 2 + y 2 2

Passo 2

A integral de linha vai ficar

I = ∮ C F ∙ d r = ∬ D 4 x y x 2 + y 2 2 d A

Temos que entender como é a região D

Repara que a região vai ser entre as circunferências de raio 1 e 2 , e limitada por x ≥ 0 e y ≥ 0 porque está no primeiro quadrante. Então a região fica assim

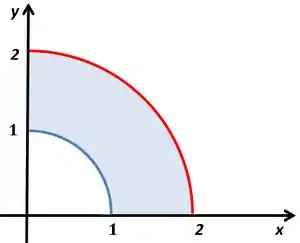
Como temos muitos x 2 + y 2 vamos usar coordenadas polares

Passo 3

Em coordenadas polares

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

Passo 4

Vamos ver os intervalos de r e θ . Como ele está entre uma circunferência e outra vamos ter

r ∈ 1,2

E como ele está limitado ao primeiro quadrante vamos ter

θ ∈ 0 , π 2

A integral vai ficar

∬ D 4 x y x 2 + y 2 2 d A = ∫ 0 π 2 ∫ 1 2 4 r cos ⁡ θ r sen ⁡ θ r cos ⁡ θ 2 + r sen ⁡ θ 2 2 r d r d θ

⇒ ∫ 0 π 2 ∫ 1 2 4 r 2 cos ⁡ θ sen ⁡ θ . r r 2 cos 2 ⁡ θ + r 2 sen 2 ⁡ θ 2 d r d θ

⇒ ∫ 0 π 2 ∫ 1 2 4 r 3 cos ⁡ θ sen ⁡ θ r 2 cos 2 ⁡ θ + sen 2 ⁡ θ 2 d r d θ

⇒ ∫ 0 π 2 ∫ 1 2 4 r 3 cos ⁡ θ sen ⁡ θ r 2 2 d r d θ

⇒ ∫ 0 π 2 ∫ 1 2 4 r 3 cos ⁡ θ sen ⁡ θ r 4 d r d θ

⇒ ∫ 0 π 2 ∫ 1 2 4 cos ⁡ θ sen ⁡ θ r d r d θ

Lembrando que 2 sen ⁡ θ cos ⁡ θ = sen ⁡ 2 θ

⇒ ∫ 0 π 2 ∫ 1 2 2 sen ⁡ 2 θ r d r d θ

Integrando

⇒ ∫ 0 π 2 2 sen ⁡ 2 θ ln ⁡ r r = 1 2 d θ

⇒ ∫ 0 π 2 2 sen ⁡ 2 θ ln ⁡ 2 - ln ⁡ 1 d θ

⇒ ∫ 0 π 2 2 sen ⁡ 2 θ ln ⁡ 2 d θ

⇒ 2 ln ⁡ 2 ∫ 0 π 2 sen ⁡ 2 θ d θ

Integrando

⇒ 2 ln ⁡ 2 - cos ⁡ 2 θ 2 θ = 0 π 2

⇒ 2 ln ⁡ 2 - cos ⁡ 2 π 2 2 - - cos ⁡ 2 . 0 2 2

⇒ 2 ln ⁡ 2 - cos ⁡ π 2 - - cos ⁡ 0 2

⇒ 2 ln ⁡ 2 - - 1 2 - - 1 2

⇒ 2 ln ⁡ 2 1 2 + 1 2

⇒ 2 ln ⁡ 2 1

⇒ 2 ln ⁡ 2

Resposta

2 ln ⁡ 2

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x