Seja o arco de círculo com centro na origem e raio 2 orientado no sentido anti-horário do ponto até o ponto e seja tal que
a) Escreva uma parametrização para e calcule
b) Complete o arco com segmentos ao longo dos eixos cartesianos de modo que a concatenação das curvas seja uma região fechada orientada no sentido anti-horário e calcule
c) Utilizando o Teorema de Green e as integrais calculadas no item (b), calcule
Passo 1
Letra a)
Como ele nos disse que é um arco de círculo de raio 2 vamos usar a parametrização:
Vamos agora ver os limites em teta dessa parametrização:
Para o ponto :
e
Para o ponto :
e
Nossa parametrização será
OBS.: O nosso sentido trigonométrico já é anti-horário então já está condizente com o sentido do problema
Passo 2
Vamos agora calcular a nossa integral de linha usando a fórmula que já conhecemos
Onde e são os extremos da minha parametrização
Derivando a função
Agora substituindo tudo na integral:
Manipulando agora a nossa integral, lembrando que :
Como se trata de um produto escalar:
Integrando agora com relação a
Passo 3
Letra b)
A curva vai ser uma curva assim
A questão pediu que completássemos o arco com mais duas curvas e ao longo dos eixos cartesianos. O que precisamos é de uma curva que ligue o ponto a origem e outra curva que ligue a origem ao ponto (-2,0).
Vamos começar por
Concorda que a curva mais simples para ligar os pontos que queremos é o segmento de reta que vá de até a origem. A nossa parametrização então pode ser:
Para :
Porém precisamos nos atentar ao sentido em que as curvas estão. Como a questão pede que a concatenação das curvas esteja no sentido anti-horário. Precisamos então que a curva esteja para cima e a curva esteja para a esquerda.
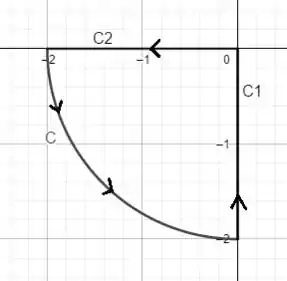
A curva do jeito que está parametrizada já está no sentido correto, porém precisamos inverter o sentido da curva .
Atenção que eu tive que mudar tanto as coordenadas quanto o meu domínio!
Passo 4
Vamos agora calcular as integrais das curvas e
Sabemos que:
Para
Substituindo para a nossa parametrização, sabendo que
Para :
Substituindo para a nossa parametrização, sabendo que
Passo 5
Letra c)
O teorema de Green relaciona a integral de linha de uma curva fechada com a integral dupla sobre a área limitada por essa curva.
Temos a fórmula que é a seguinte:
Aqui atenção que na representação, é a área da região enquanto que é o contorno dessa região.
A integral da esquerda é a soma das integrais de linha de cada curva
Já calculamos as integrais para e que são iguais a 0. Sobrando exatamente a integral que o problema nos pede.
Vamos agora para a integral do lado direito do Teorema de Green
Lembrando que .
Logo, e
Primeiro vamos derivar parcialmente em relação à x:
E então, vamos derivar parcialmente em relação à y:
Voltando para a integral teremos:
Passo 6
Para resolver essa integral, vamos fazer a mudança para coordenadas polares
Vamos investigar agora nossos limites:
Para :
Temos uma circunferência de raio 2 então nosso raio vai variar
Para
Já sabemos que a nossa região varia de um teta
Substituindo tudo isso na nossa integral
Esse que aparece no final é por conta do Jacobiano
Vamos manipular um pouco
Perceba que não tem nada dependendo de teta, então para facilitar, vou resolver a integral mais externa primeiro
Essa integral não parece nada legal, não é mesmo?? Mas percebe que o problema nos deu uma dica, então vamos tentar manipular a nossa integral para podermos usar essa dica. Por esse motivo, vou manter o 2 no integrando.
Separando a nossa integral em duas ficamos com:
Da dica temos que que é exatamente a primeira integral. Ficamos então com
Vamos resolver agora para a segunda integral:
Usando uma mudança de variável:
Então o nosso resultado será:
Ufa!!! Bateu com o nosso resultado da letra (a), que era o esperado.
Resposta
Letra a.
Letra b.
Letra c.