UFAM– Cálculo 2 – P3 – Questão 5
Calcule a integral de linha , onde é o círculo com orientação positiva.
Passo 1
Oi, tudo bem?
O problema nos pediu para calcularmos essa integral de linha
Onde a curva C é um círculo
E tem orientação positiva! Se tem orientação positiva e é uma região fechada: TEOREMA DE GREEN!
Esse teorema é muito maneiro! Ele transforma uma integral de linha complicada (tenta fazer por parametrização, você vai ver que fica muito mais complicado!) em uma integral de área mais simples. Mas como assim transforma? Assim:
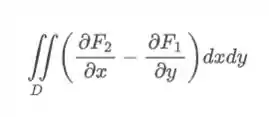
E quem são esses e ? São as funções que multiplicam e no nosso integrando respectivamente!
Assim e
então a ideia para resolver essa questão é:
- Identificar quem são , derivar conforme o teorema manda e substituir no integrando
- Arrumar os limites de integração: aqui vou integrar usando coordenadas polares, pois a integração fica beeem mais fácil
- Por fim, partiu integrar!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
No primeiro passo já identifiquei com você as funções e :
Relembrando que tiramos elas da nossa integral de linha:
ok? Agora vamos aplicar as derivadas que o teorema manda:
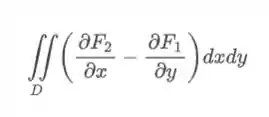
assim temos
Beleza? E agora vamos substituir na integral dupla:
Tranquilo até aqui?
Passo 3
Agora vamos arrumar os limites de integração!
A região é um círculo de raio 2 centrada na origem:
Passando para coordenadas polares:
Então o raio vai de até , e o ângulo de até .
O diferencial de área era , mas agora em polares fica .
E nosso integrando? Nossa integral era assim:
Mas substituindo , o integrando fica assim:
Tudo bem até aqui?
E com os limites de integração, nossa integral de linha vira essa integral aqui de área:
Vamos calcular essa integral? Bora lá!
Passo 4
Como não temos função/limite de integração, nada que dependa de , então podemos transferir o para a última integral (a mais de fora) e já resolver. Podemos também resolver a mais interna (que depende de ), tudo junto. Aí temos o seguinte
Agora é só aplicar nos limites:
Ufa! Agora sim! Terminamos! Espero ter ajudado!
Até próxima!