Calcule a integral de linha do campo vetorial ao longo da curva , sendo o bordo da região definida pela interseção das seguinte regiões , , e . Além disso, assumimos que é orientada no sentido horário.
Passo 1
Temos parábolas limitando a seguinte região:
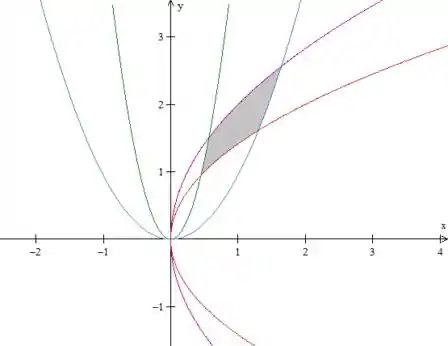
Como a integral ao longo dessa curva parece complicada de se calcular pela definição, vamos aplicar o Teorema de Green. Como está orientada negativamente, temos:
Passo 2
Vamos agora calcular :
Passo 3
Aplicando o teorema de Green, temos:
Passo 4
Parece complicado descrever a região em termos de e , vamos então fazer uma mudança de variáveis. Como temos parábolas descritas por e outras por e, vamos chamar:
Passo 5
Precisamos calcular o Jacobiano dessa mudança. Como é complicado escrever e em função de e , vamos calcular o Jacobiano da transformação inversa, e inverter o resultado:
Passo 6
Agora temos que encontrar os intervalos de integração em e . Fazendo a substituição de variáveis das equações das parábolas temos:
Ou seja, e .
Passo 7
Substituindo os valores que encontramos na integral, temos:
Passo 8
Integrando em relação a :
Passo 9
Agora em relação a :