Calcule a integral de linha
Em que é a curva fronteira da região englobada pelas parábolas e com orientação positiva
Passo 1
Bem a primeira coisa que conseguimos perceber é que ele quer essa integral de linha vetorial que está ali.
Olha as funções que estão nessa integral
Repara que essas funções são estranhas né? Aquela raiz no exponencial, o cosseno de . A região que ele pediu não é muito complexa, são duas parábolas de boa, mas essas funções e são deveras estranhas. Então vamos tentar aplicar o teorema de Green para facilitar nossas contas, pode ser que não ajude e tenhamos que voltar para a conta normal na marra, mas vamos tentar primeiro né? Para isso devemos calcular
Então
Vamos ter
Opa, deu um número, e além disso ele disse que a orientação é positiva, ou seja, vamos aplicar Green nesse, lembra como ele é?
Onde é a região que tem fronteira , no nosso caso vamos ter
Transformamos essa integral de linha louca em uma integral dupla tranquilinha.
Passo 2
Vamos agora resolver
Mas primeiro temos que entender como é essa região , vamos fazer um esboço das duas parábolas.
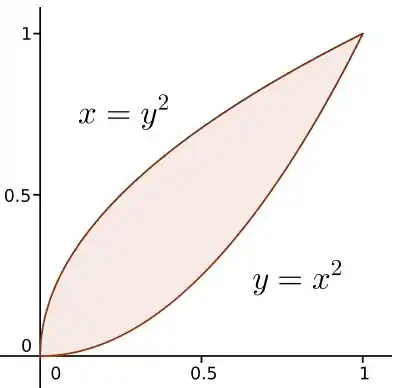
Como vamos garantir esse pontos onde elas se encontram? Vamos resolver o sistema eu
Substituindo o valor de da equação de baixo na de cima vamos ter
Então
Além disso vamos ter
Os pontos são e
E achamos os pontos direitinho.
Essa região pode ser vista tanto como Tipo I como Tipo II, na realidade não faz diferença nenhuma qual escolhermos as contas vão ficar praticamente idênticas. Eu vou fazer por Tipo I, simplesmente porque I vem antes do II rs, faz sentido? Nenhum né? Mas como não faz diferença n importa.
Repara que vai da parábola de baixo até a parábola de cima, enquanto o vai de à .
Vamos escrever em função de nas duas parábolas, começando com a de cima, ele disse que
Então
Pegamos a parte positiva dessa parada porque como podemos ver queremos a parte no primeiro quadrante do plano cartesiano, onde e
Então
A parábola de baixo vai ficar
E já está bonitinho.
A região vai ser
Passo 3
Vamos agora para integral, ela vai ficar
Então vamos ter