Se uma circunferência de raio rola ao longo do exterior da circunferência , um ponto fixo de descreve uma curva chamada epiciclóide. Uma parametrização da epiciclóide é dada por . Nessa parametrização é uma curva fechada para . Calcule a área da região limitada pela epiciclóide .
Passo 1
Imagino que você tenha lido esse enunciado e pensado “wtf”. Calma, não é tão ruim assim. Isso não é fundamental para a questão, mas só para a gente entender melhor, essa curva que o enunciado chama de “epiciclóide” é isso aqui:
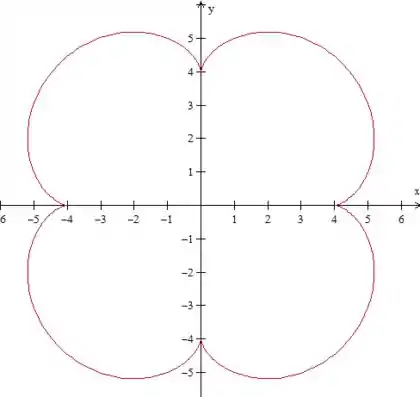
Como a questão fala, ela é fechada. É disso que precisamos saber.
Passo 2
Certo, agora queremos a área disso aí. Vamos pensar com muita calma. Nós queremos a área de uma região limitada por uma curva (que está parametrizada).
Bom, falando em área nós pensamos logo em integral dupla, né?
Que Teorema que nós conhecemos que relaciona uma integral dupla em uma área com a sua fronteira? No caso, com uma integral de linha sobre sua fronteira.
Isso mesmo, Teorema de Green:
Olha que maravilha, já é fechada. Então, podemos relacionar uma integral de linha sobre com uma integral dupla na área limitada por ela.
Mas temos um problema, aquela integral dupla que apareceu no teorema não é igual à área, que queremos.
Na verdade, ela pode ser igual se:
Então, tudo o que precisamos é de um campo que satisfaça essa condição. Vamos escolher um fácil né? Pode ser:
Nesse caso
Show! Agora podemos aplicar Green:
Logo, a área que queremos é dada pela integral de linha de (que inventamos) em .
Passo 3
Como a curva já está parametrizada, a primeira coisa a fazer para montar a integral de linha é derivar essa parametrização:
Passo 4
Agora, vamos aplicar a fórmula:
Escrevendo o campo nas variáveis da parametrização, temos:
Levando o que temos para a integral
Agora, usamos a relação
Assim, temos