Considere o campo vetorial em .
Calcule
Onde é o quadrado de vértices , , , , percorrido no sentido anti-horário.
Passo 1
Bem, como a região limitada por é um quadrado (bem simples de se escrever em integral duplas), vamos tentar aplicar Green para ver no que dá:
Passo 2
Agora vamos dar uma olhada nessa curva . Temos isso aqui:
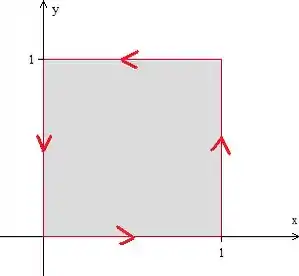
Beleza, como a curva está orientada positivamente e o campo está definido dentro dela, podemos escrever o seguinte:
Ou seja:
Passo 3
Agora vamos escrever essa região na integral dupla, o que é bem tranquilo, porque se trata de um quadrado:
Resolvendo isso aí: