Considere o campo vetorial dado por , onde . Calcule , onde é a elipse , percorrida no sentido anti-horário.
Passo 1
Esse enunciado é meio estranho, não é? Parece que as informações estão todas meio confusas ai dentro. Vamos tentar esclarecer tudo o que ele nos informou:
A primeira coisa que ele faz é definir o campo vetorial
Isso que ele fez é praticamente definir o campo como uma subtração de dois campos, pensa em nesse caso
Tá, e o que é esse triangulo de cabeça pra baixo aí? Isso é um operador que a gente conhece por
Ou seja, ele transforma uma função em um vetor de derivadas! A primeira em relação a e a segunda em relação a , sacou?
Isso vai ser muito útil pra gente quando formos calcular o termo da integral dupla de green, mas a gente já chega lá! :D
Passo 2
Beleza, vamos voltar então pro que o enunciado pede. Ele quer que a gente calcule
Como desmembramos o campo , o que precisamos calcular é isso aqui
Vamos fazer cada uma separadamente aqui, beleza? Mas... a dificuldade maior mesmo é entender esses detalhes. É uma questão bem diferente que, se deixamos passar alguma coisa, não vamos conseguir resolver. E e ntão você entendeu???
Se sim, me siga ;)
Se não, dá mais uma lidinha. Confio em você e você vai entender :D!
Passo 3
Vamos partir aqui para a primeira integral
Pelo teorema de Green
E aqui que vamos ter uma sacada, dá uma olhada com atenção nisso aqui
Ou seja, é a derivada de em relação a e vamos deriva-la em relação a agora. Algo semelhante vai acontecer com
Só que aprendemos lá no começo de derivadas uma propriedade que vai nos salvar aqui! Quando temos uma função contínua num intervalo dado, temos a igualdade
Ou seja, derivar a função primeiro em e depois em é a mesma coisa que primeiro em e depois em ! Agora ficou moleza, né? Como esses dois caras são iguais
E a integral fica
Felicide tentendo ao infinito nesse momento, neh?
Passo 4
Vamos agora para a integral de
É só fazer o teorema de Green normalmente aqui, como nossa curva é fechada, fica assim
Vamos calcular esse termo dentro da integral dupla, então
A integral fica
Só que a região é essa elipse aqui
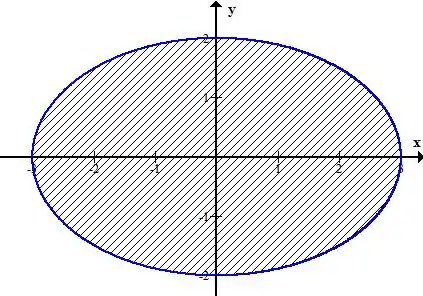
Para uma elipse genérica
Podemos calcular a sua área através da frmula
No nosso caso a elipse tem e , portanto
Passo 5
Voltando para a pergunta dele lá do começo