Considere a integral de linha
Onde é a curva que delimita a região entre os gráficos de e .
- Calcule usando obrigatoriamente o Teorema de Green.
- Confira o resultado do item anterior calculando pela definição.
Passo 1
Letra a)
Bom, para aplicar Green, precisamos começar calculando o termo :
Passo 2
Agora vamos dar uma olhada nessa região , temos uma parábola com concavidade para baixo cortada pela reta :
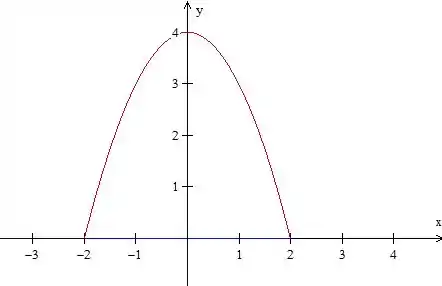
A curva do problema é essa aí, para podermos aplicar Green, vamos orientá-la dessa forma:
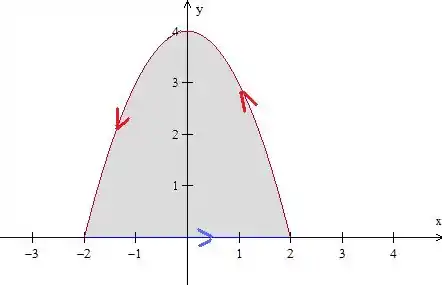
Beleza, como a curva está orientada positivamente e o campo está definido em , podemos escrever o seguinte:
Ou seja:
Passo 3
Agora vamos escrever essa região como tipo I e resolver essa integral.
Temos entre as curvas e , enquando varia de a , como vemos na figura. Levando isso para a integral:
Agora é só resolver isso aí:
Passo 4
Letra b)
Beleza, agora vamos calcular essa integral de linha pela definição. Antes de tudo, precisamos parametrizar , que é formada por duas curvas com equações diferentes.
Vamos chamar a parábola de e o segmento de reta de ok? Portanto, é a união de com .
Vamos parametrizar a parábola usando como parâmetro, para facilitar as coisas. Temos isso aqui:
Como podemos ver pelo gráfico, vai de a (respeitando a orientação da curva).
Como o segmento de reta pertence à reta , podemos usar essa parametrização aqui:
Olhando de novo para o gráfico, temos de a
Passo 5
Agora vamos derivar essas parametrizações aí:
Passo 6
Show, agora vamos montas as integrais, temos isso aqui:
Mas é formada por duas partes:
Substituindo o que encontramos nos outros passos e escrevendo o campo
em função das variáveis de cada parametrização, temos:
Para a primeira integral, temos:
Para a segunda integral:
Logo:
Ótimo, encontramos a mesma coisa : )