Questão 4: Use o teorema de Green para calcular a integral de linha da função vetorial
onde é o bordo da região delimitada por e , orientado no sentido anti-horário.
Passo 1
Antes de apresentar a igualdade do Teorema que vamos utilizar, que tal mudarmos a notação dessa integral de linha?
Onde . É a mesma coisa só que escrita de uma forma mais “enxuta”!
Pois bem, o maravilhoso Teorema de Green nada mais é do que essa igualdade linda aqui:
Agora, para aplicar tal igualdade, temos que ter algumas hipóteses satisfeitas. Para verificar, venha comigo!
Passo 2
As três hipóteses do Teorema, basicamente são:
- Curva fechada e delimitando .
- Orientada positivamente.
- Campo sem singularidades.
No nosso caso, todas elas estão sendo satisfeitas pelo problema, mas para verificar, me acompanhe nos próximos passos!
Passo 3
Quanto à curva fechada, isso acontece já que ela é borda de uma região limitada. Podemos desenha-la para conferir!
Colocando as e no plano...
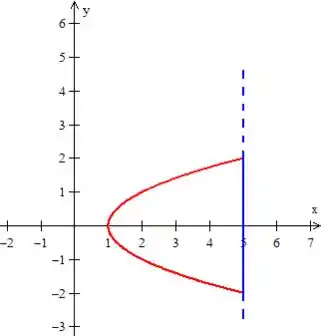
Olha a região aí no interior:
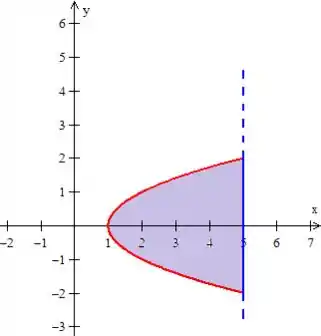
Passo 4
Para a orientação positiva, precisamos da curva girando no sentido anti-horário:
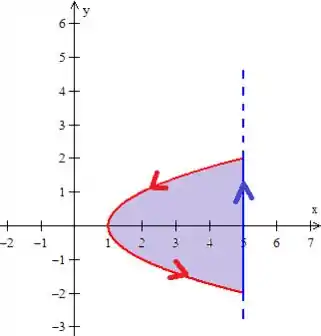
O que acontece já desde o enunciado!
Passo 5
Para a última análise, temos que verificar se o campo não possui nenhuma singularidade no interior de onde estamos trabalhando:
Veja que ele é formado apenas por termos que são contínuas em qualquer ponto do plano! Logo, essa última hipótese também está ok!|
Passo 6
Com essas três análises, podemos finalmente aplicar a igualdade do teorema como o enunciado nos pede para resolver a integral de linha:
Calculando então essas derivadas parciais dado que:
Logo, a integral dupla que precisaremos resolver é:
Vamos nessa?
Passo 7
Para calcular tal integral, a primeira coisa a se fazer é descrever a região :
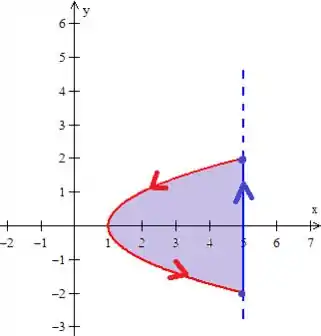
Veja que podemos fazer isso utilizando a classificação em região do tipo , onde varia da parábola à reta, enquanto o varia entre o ponto (bolinha) de baixo em azul, ao ponto de cima:
A parábola possui equação e a reta :
Enquanto os pontos para os limites de , são provenientes da intersecção entre a reta e parábola:
Então...
Passo 8
Finalmente, calculando a integral dupla:
Simplificando...