Sejam e uma função não nula de classe . Considere as seguintes afirmações:
- Se , para todo então para toda circunferência .
- Se para todo , então para toda curcunferência vale que
- Se é a cirncunferência percorrida uma única vez no sentido horário e é a mesma circunferência percorrida uma única vez no sentido anti-horario, então
Para toda função como acima:
Passo 1
- Se , para todo então para toda circunferência .
Falso! Observa que essa afirmação só é verdadeira quando:
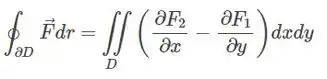
No entanto, pra isso acontecer existem algumas condições;
- Curva fechada: o que está ok, já que estamos trabalhando com uma circunferência
- Campo sem singularidade: não temos nenhuma garantia disso
- Orientação positiva: depende então também da orientação dessas circunferencias
Passo 2
Fazendo
Parametrizando a curva:
Termo ds:
Montando a integral:
Afirmativa errada.