Exercícios de Velocidade Angular e Aceleração Angular Instantâneas - Lista de Exercícios Resolvida

Durante um intervalo de tempo t, o volante de um gerador gira de um ângulo e , onde , e são constantes. Escreva expressões para o vetor velocidade angular

A posição angular de um ponto sobre uma roda que está girando é dada por , onde está em radianos e em segundos. Em , qual é a posição angular do ponto ?

A posição angular de um ponto de uma roda é dada por , onde está em radianos e em segundos. Em , qual é:

a) a posição angular no ponto?

b) a velocidade angular do ponto?

c) Qual éa velocidade angular em ?

d) Calcule a aceleração angular em .

e) A aceleração angular da roda é constante?

Um objeto gira em torno de um eixo fixo e a posição angular de uma reta de referência sobre o objeto é dada por , onde está em radianos e em segundos. Considere um ponto do objeto situado a do eixo de rotação . Em , qual é o módulo

a) da componente tangencial no ponto?

b) da componente radial da aceleração do ponto?

Uma partícula tem uma aceleração angular que varia com o tempo conforme a equação: .

a) Encontre a velocidade angular em função do tempo .

b) Encontre o valor dessa aceleração e da velocidade angular no instante t=2s.

A aceleração angular de uma roda é , com em radianos por segundo ao quadrado e tem segundos. No instante , a roda tem uma velocidade angular de e uma posição angular de . Escreva expressões

a) para a velocidade angular (em ) e

b) para a posição angular (em ) em função do tempo (em ).

Uma partícula tem sua posição angular que varia com o tempo conforme a equação: .

1. Encontre a velocidade angular em função do tempo .
2. Encotnre a aceleração angular em função do tempo

c) Encontre o a posição, a velocidade e a aceleração angular no instante t=1s.

Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, partindo do repouso, gira de acordo com a equação , onde está em segundos e em radianos. No instante , calcule o módulo

a) da velocidade angular

b) da velocidade linear

c) da aceleração tangencial

d) da aceleração radial do astronauta

(Cap 11 – Ex 2) Um automóvel que se move a possui pneus com de diâmetro.

a) Qual é a velocidade angular dos pneus em relação aos respectivos eixos?

b) Se o carro é freado com aceleração constante e as rodas descrevem voltas completas (sem deslizamento), qual é o módulo da aceleração angular das rodas?

c) Que distância o carro percorre durante a frenagem?

(Cap 11.4 – Ex 9) Na Fig. 11-33, um cilindro maciço com de raio e uma massa de parte do repouso e rola para baixo uma distância , sem deslizar, em um telhado com uma inclinação .

a) Qual é a velocidade angular do ciclindro em relação ao eixo central ao deixar o telhado?

b) A borda do telhado está a uma altura . A que distância horizontal da borda do teto o cilindro atinge o chão?

As lâminas de um ventilador giram com velocidade angular dada por , onde e . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceleração angular instantânea , para e a aceleração angular média, , para o intervalo de até . Como essas duas grandezas podem ser comparadas? Caso elas sejam diferentes, por que são diferentes?

A peça de uma máquina tem o formato de uma esfera maciça e uniforme com massa de e o diâmetro de . Ela está girando em torno de um eixo com atrito desprezível que passa pelo seu centro, mas em um ponto no seu equador ela está roçando contra uma parte metálica, resultando em uma força de atrito de neste ponto.

Ache a aceleração angular.

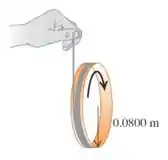
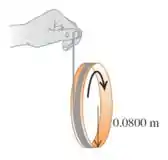
Um fio é enrolado diversas vezes em torno da periferia de um pequeno aro de raio e de massa . A extremidade livre do fio é mantida fica e o aro é liberado a partir do repouso (figura abaixo). Após o aro cair por , calcule

a velocidade escalar angular do aro em rotação

(Cap 10 – Ex 11) Um tambor gira em torno do eixo central com uma velocidade angular de . Se o tambor é freado a uma taxa constante de ,

(a) quanto tempo leva para parar?

(b) Qual é o ângulo total descrito pelo tambor até parar?

(Capítulo 10.4 – Ex. 16) Um disco gira em torno do eixo central partindo do repouso com aceleração angular constante. Em um certo instante, está girando a ; após 60 revoluções, a velocidade angular é . Calcule (a) a aceleração angular, (b) o tempo necessário para completar 60 revoluções, (c) o tempo necessário para atingir a velocidade angular de e (d) o número de revoluções desde o repouso até o instante em que o disco atinge uma velocidade angular de .

A velocidade angular de um volante obedece à equação , onde está em segundos e e são constantes, com valores numéricos de e .

a) Quais são as unidades de e de , se está em ? b) Calcule a aceleração angular do volante para . c) Qual é o ângulo em que o volante gira durante os primeiros ?

Um foguete é lançado de um ângulo do topo de uma torre com altura . Devido ao design das engrenagens, suas coordenadas são da forma e onde e são constantes. Além disso, a aceleração do foguete após o lançamento é . Use a origem do eixo de coordenadas como a base da torre.

(b) No instante após o lançamento do foguete, quais são seus vetores aceleração e velocidade?

Para , a roda de um esmeril possui velocidade angular igual a . Ela possui uma aceleração angular constante igual a , quando um freio é acionado em . A partir desse instante ela gira à medida que para com uma aceleração angular constante.

a) Qual foi o deslocamento angular total da roda desde até o instante em que ela parou?

Para , a roda de um esmeril possui velocidade angular igual a . Ela possui uma aceleração angular constante igual a , quando um freio é acionado em . A partir desse instante ela gira à medida que para com uma aceleração angular constante.

b) Em que instante ela parou?

Para , a roda de um esmeril possui velocidade angular igual a . Ela possui uma aceleração angular constante igual a , quando um freio é acionado em . A partir desse instante ela gira à medida que para com uma aceleração angular constante.

c) Qual foi o módulo da sua aceleração quando ela diminuía de velocidade?

Uma partícula de massa executa um movimento circular, descrito pelo vetor posição

em que , com e constantes positivas.

(b) mostre que são perpendiculares ao vetor ;

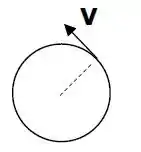
Na figura ao lado está representado numa posição, o vetor velocidade instantânea de um objeto movendo se numa trajetória circular. Se o objeto tem rapidez decrescente, em qual das figuras melhor representa o vetor aceleração a do objeto neste ponto?

Uma haste metálica fina, de comprimento e massa , pode girar em torno de um eixo horizontal que a atravessa perpendicularmente (saindo da página), à distância de sua extremidade (ver figura ao lado). A haste é solta a partir do repouso de sua posição horizontal. Calcule:

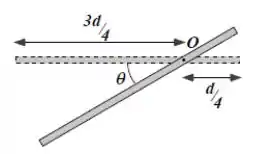
b) As velocidades lineares do centro de massa e das extremidades da barra quando

Uma partícula de massa executa um movimento circular, descrito pelo vetor posição

em que , com e constantes positivas.

(a) Determine os vetores velocidade, , e aceleração ;

Uma criança empurra um carrossel, cujo deslocamento angular varia no tempo de acordo com a relação: . Nessas condições, qual a velocidade angular média do carrossel no intervalo de até ? Quantas voltas o carrossel dá no intervalo de até ?

(Aproxime por 3)

(a) e voltas.

(b) e voltas.

(c) e voltas.

(d) e voltas.

(e) e voltas.

Uma partícula executa o movimento espiral mostrado na figura com e onde , e são constantes positivas. Marque a opção correta abaixo que descreve o movimento quando :

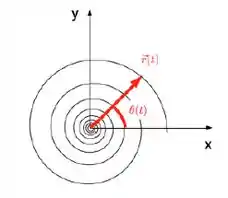
(a) Aceleração radial e a velocidade radial decrescem exponencialmente.

(b) Aceleração radial é nula enquanto a velocidade radial é nula.

(c) Aceleração radial cresce exponencialmente enquanto a velocidade radial decresce linearmente no tempo.

(d) Aceleração radial e a velocidade radial crescem exponencialmente.

(e) Aceleração radial é nula enquanto a velocidade radial cresce exponencialmente.

No filme “Tempos Modernos”, o personagem Carlitos trabalha sobre uma engrenagem bastante complexa como mostra a figura a seguir:

Considere as rodas dentadas identificada por e na figura. O raio da roda é e o da roda de . Despreze todas as interações com as demais rodas. A roda partindo do repouso () com aceleração angular constante, leva para atingir sua velocidade final de funcionamento e efetua um total de rotações durante este intervalo. Qual o módulo da aceleração linear da roda em durante este intervalo?

Escolha uma:

Não é possível calcular a aceleração somente com os dados fornecidos.

Nenhuma das outras alternativas está correta.

Um pulsar é uma estrela de nêutrons que gira rapidamente em tomo de si mesma e emite um feixe de rádio, do mesmo modo como um farol emite um feixe luminoso. Recebemos na Terra um pulso de rádio para cada revolução da estrela. O período de rotação de um pulsar é determinado medindo o intervalo de tempo entre os pulsos. O pulsar da nebulosa do Caranguejo tem um período de rotação que está aumentando a uma taxa de .

(a) Qual é a aceleração angular a do pulsar?

(b) Se a se mantiver constante, daqui a quantos anos o pulsar vai parar de girar?

(c) O pulsar foi criado pela explosão de uma supemova observada no ano de 1054. Supondo que a aceleração a se manteve constante, determine o período T logo após a explosão.

Um fio é enrolado diversas vezes em torno da periferia de um pequeno aro de raio e de massa . A extremidade livre do fio é mantida fica e o aro é liberado a partir do repouso (figura abaixo). Após o aro cair por , calcule

a velocidade escalar no seu centro

Um corpo inicialmente em repouso, é acelerado em uma trajetória circular de raio , segundo a equação . Sabe-se que a partícula passa pela posição em . Determinar:

(c) As componentes tangencial e centrípeta de sua aceleração.

Um corpo inicialmente em repouso, é acelerado em uma trajetória circular de raio , segundo a equação . Sabe-se que a partícula passa pela posição em . Determinar:

(a) A velocidade angular do corpo em função do tempo;

(Cap 10 – Ex 17) Uma roda executa revoluções quando desacelera a partir de uma velocidade angular de até parar.

a) Supondo que a aceleração angular é constante, determine o tempo em que a roda leva para parar.

b) Qual é a aceleração angular da roda?

c) Quanto tempo é necessário para que a roda complete as primeiras revoluções?

(Cap 10 – Ex 9) Um disco, inicialmente girando a , é freado com uma aceleração angular constante de módulo

(a) Quanto tempo o disco leva para parar?

(b) Qual é o ângulo total descrito pelo disco durante esse tempo?

(Cap 10 – Ex 12) Partindo do repouso, um disco gira em torno do eixo central com uma aceleração angular constante. O disco gira em . Durante esse tempo, qual é o módulo

(a) da aceleração angular e

(b) da velocidade angular média?

(c) Qual é a velocidade angular instantânea do disco ao final dos ?

(d) Com a aceleração angular mantida, que ângulo adicional o disco irá descrever nos seguintes?

(Cap 10.2 – Ex. 1) Um bom lançador de beisebol pode arremessar uma bola a com uma rotação de . Quantas revoluções a bola realiza até chegar à base principal? Para simplificar, suponha que a trajetória de pés é percorrida em linha reta.

(Cap 10 – Ex 57) Uma polia, com um momento de inércia de em relação ao eixo e um raio de , é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo com a equação , com em newtons e em segundos. A polia está inicialmente em repouso. Em , quais são

a) a sua aceleração angular e

b) sua velocidade angular?

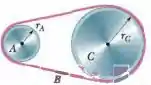
(Cap 10.5 - Ex. 30) Na Fig. 10-32, uma roda de raio está acoplada por uma correia a uma roda de raio . A velocidade angular da roda é aumentada a partir do repouso a uma taxa constante de . Determine o tempo necessário para que a roda e atinja uma velocidade angular de , supondo que a correia não desliza. (Sugestão: se a correia não desliza, as velocidades lineares das bordas dos discos são iguais.)

Uma bolinha está sobre um aro circular de raio que roda em torno do diâmetro com velocidade . Não há atrito.

• Qual deve ser a velocidade que mantém a bolina na mesma posição do aro, um ângulo com respeito a vertical?
• Analise a resposta anterior: Haverá um intervalos de velocidades angulares , para uma ângulo fixo . Descubra o valor de .

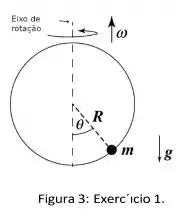
Adote as constantes citadas no exercício em suas respostas e como a magnitude da constante da aceleração da gravidade.

Uma porta de e de largura, suspensa por dobradiças bem azeitadas, está aberta de , ou seja, com seu plano perpendicular ao plano do batente. Ela leva um empurrão na beirada aberta, com impacto equivalente ao de uma massa de com velocidade de . Quanto tempo ela leva para fechar-se?

34. Uma mesa de coquetel tem um tampo giratório, que é uma tábua circular de raio e massa , capaz de girar com atrito desprezível em torno de um eixo vertical da mesa. Uma bala de massa e velocidade , disparada por um convidado, numa direção horizontal, vai encravar-se na periferia da tábua.

(a) Qual é a velocidade angular de rotação adquirida pela tábua?

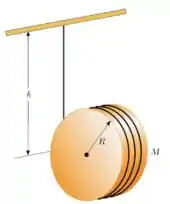
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.

(c) Qual é a velocidade do centro de massa depois que o disco desce uma distância vertical ?

42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .

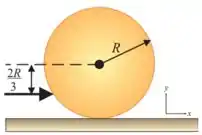
(a) Qual a velocidade angular inicial ?

41. Uma bola homogênea de raio rola sem deslizar, a partir do repouso, desde o topo de um domo hemisférico de raio .

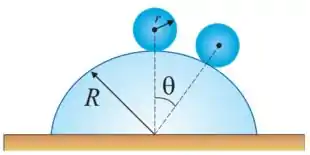
(b) Com que velocidade isso acontece?

42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .

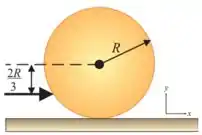
(b) Qual a velocidade da bola uma vez iniciado o rolamento sem escorregamento?

Uma lâmina rotatória de um misturador gira com aceleração angular constante igual a

a) Partindo do repouso, quanto tempo ela leva para atingir uma velocidade angular de ?

Uma lâmina rotatória de um misturador gira com aceleração angular constante igual a .

b) Qual o número de revoluções descritas pela rotação da lâmina nesse intervalo de tempo?

Um foguete é lançado de um ângulo do topo de uma torre com altura . Devido ao design das engrenagens, suas coordenadas são da forma e onde e são constantes. Além disso, a aceleração do foguete após o lançamento é . Use a origem do eixo de coordenadas como a base da torre.

(c) Quais são as componentes e da velocidade do foguete após o lançamento, e quão rápido ele está se movendo?

Q - Um corpo, partindo do repouso, percorre uma trajetória circular de raio , levando para completar a primeira volta. Sabendo que a aceleração angular é mantida constante, o intervalo de tempo (em segundos), a partir do início do movimento, gasto para percorrer um arco de comprimento igual a é:

Um corpo em rotação tem posição angular em radianos e em segundos. Então, sua velocidade angular instantânea em , será:

a) -7 rad/s

b) 13 rad/s

c) - 23 rad/s

d) 7,29 rad/s

e) 6 rad/s

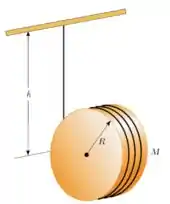
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.

(b) Qual é o módulo da aceleração do centro de massa?

2) Um trem viaja para o norte a . A fumaça da locomotiva forma uma trilha que se estende numa direção a leste da direção sul, com o vento soprando do Oeste. Qual a velocidade do vento?

3) Um avião leve atinge uma velocidade no ar de . O piloto pretende chegar a um ponto ao norte, mas descobre que deve direcionar o avião a a leste do norte para atingir seu destino. O avião chega em . Quais eram (a) o módulo e (b) a orientação da velocidade do vento?

4) Um menino faz uma pedra descrever uma circunferência horizontal com de raio, acima do chão. A corda se rompe e a pedra é arremessada horizontalmente, chegando ao solo depois de descrever uma distância horizontal de . Qual era o módulo da acelera��ão centrípeta da pedra durante o movimento circular?

7) Um canhão lança um projétil por cima de uma montanha de altura , de forma a passar quase tangenciando o cume no ponto mais alto de sua trajetória. A distância horizontal entre o canhão e o cume é . Atrás da montanha há uma depressão de profundidade . Determine a distância horizontal entre o ponto de lançamento e o ponto onde o projétil toca o solo.

5) Uma bola rola horizontalmente do alto de uma escada com uma velocidade de . Os degraus têm de altura e de largura. Em que degrau a bola bate primeiro?

6) A velocidade escalar de um projétil quando ele alcança sua altura máxima tem a metade do valor de sua velocidade escalar que ele tem quando está na metade da sua altura máxima. Qual o ângulo de lançamento do projétil?