Sistema de Partículas
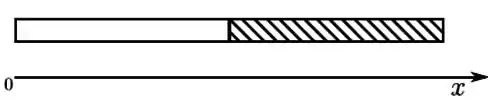
Uma barra de comprimento é formada por duas metades, como mostra a figura. A parte da esquerda possui metade da massa da parte da direita, hachurada. Separadamente, as duas partes são homogêneas. Desejamos usar um fio para prender esta barra ao teto. Para que a barra fique em equilíbrio, na posição horizontal, ela deve ser pendurada pelo ponto tal que
(a)
(b)
(c)
(d) seja qualquer entre e
(e) seja qualquer entre e
Passo 1
Para que a barra fique em equilíbrio, o fio tem que ser ligado ao centro de massa da barra. Dessa maneira a força de tração do fio não vai gerar uma rotação e vai se cancelar com a força peso.
Então vamos achar a posição do CM da barra!
O comprimento da metade esquerda da barra é , e ela é homogênea. Então o centro de massa dessa metade fica em .
Digamos que a massa dessa metade é . Então vamos considerar a massa toda concentrada em .
Pra outra metade podemos fazer a mesma coisa, a diferença é que a posição do CM é e que a massa é dobro, .
Então é como se tivéssemos 2 partículas, assim ó:
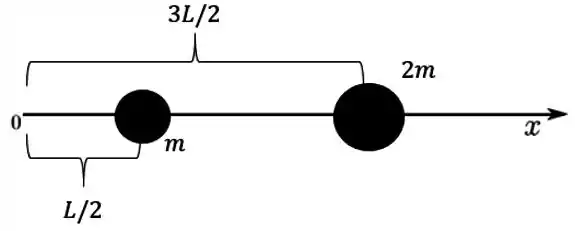
Passo 2
Agora ficou mais fácil de calcular a posição do centro de massa !
Ela é dada por:
Resposta
Alternativa (b)