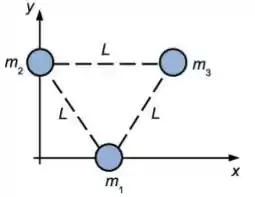
Três massas puntiformes estão localizadas nos vértices de um triângulo equilátero de lado conforme mostra a figura abaixo. Considere as seguintes situações:
as três massas são idênticas e .
Sejam e as coordenadas do centro de massa desse sistema nas situações e , respectivamente, no referencial da figura. Sobre as coordenadas do centro de massa, podemos então afirmar que:
Passo 1
Vamos calcular o centro de massa para cada situação, começando pela :
A posição era fácil por sabermos as posições de cada massa nesse eixo, porém no eixo , não sabemos a posição das partículas e .
Para descobrir essa posição usaremos o teorema de Pitágoras, pois sabemos a hipotenusa e a base falta apenas a altura.
Agora que sabemos a altura das partículas, podemos calcular a posição do centro de massa
Passo 2
Agora vamos calcular a posição do centro de massa para a situação :
Nessa situação temos que
Agora a coordena :
Passo 3
Agora faremos as razões entre as posições do centro de massa
Sendo assim, a alternativa correta é a
Resposta
Alternativa