Encontre a posição do centro de massa do objeto desenhado na figura abaixo, sabendo que ele é constituído por 6 pedações de arames homogêneo feitos do mesmo material.
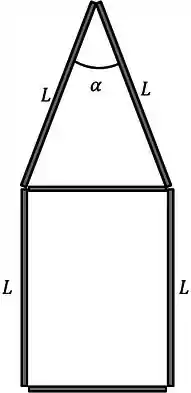
Passo 1
Assim como quando usamos fios, ao usar arames, vamos considerar em vez da massa, o seu comprimento. Isso porque a massa e o comprimento são proporcionais, então no cálculo do centro de massa não altera o resultado.
Vamos colocar o eixo cartesiano como na figura abaixo.
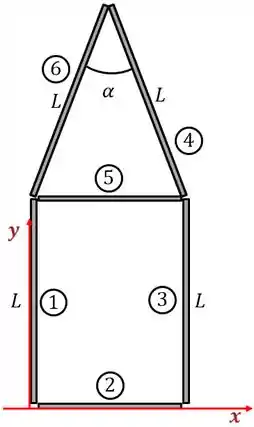
Repara que temos 6 barras, uma coisa para ajudar a organizar a resolução é nomear cada barra. Para achar o centro de massa precisamos da posição do meio de cada barra para usar na fórmula. Não temos o comprimento de todas elas.
Passo 2
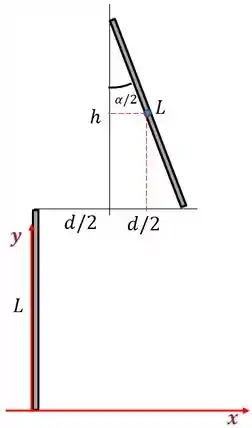
Vamos começar encontrando o comprimento das barras e . Vamos chamar seu comprimento de . Olha o triangulo
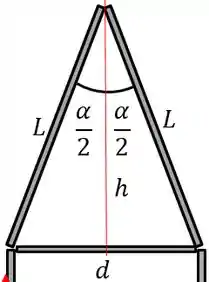
Esse triangulo é isósceles, então posso separar o ângulo como fiz na figura. Usando trigonometria encontramos
Passo 3
Vamos começar achando a posição do centro de massa da barra .
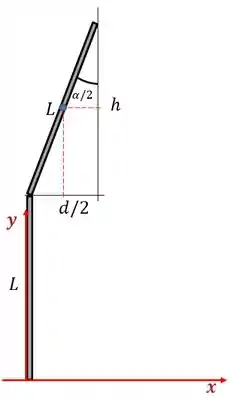
Repara que a posição vertical dele vai ser
Que é a metade da “altura” da barra mais a a altura onde a barra está .
Vamos achar então, usando trigonometria de novo
Vamos ter
Passo 4
Agora vamos achar a posição horizontal dele, que vai ser
Isso porque ela fica na metade do “comprimento” da barra, e esse “comprimento” é .
Então
É importante entender que em uma barra o centro de massa está na metade do comprimento e na metade da altura da barra.
Passo 5
Vamos agora para a barra
a altura do centro de massa dessa barra vai ser igual a da barra
Passo 6
A posição horizontal dele vai ser
Então
Passo 7
O centro de massa das outras barras é mais fácil de fazer, segue um desenho da posição de cada um
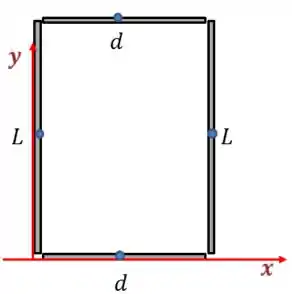
Vamos ter,
Passo 8
Vamos agora juntar isso tudo, começando pela posição horizontal
Sabemos que
Colocando o que der para colocar em evidência
Ufa né? Deixa eu te falar uma parada, eu fiz dessa forma mega trabalhosa para te mostrar como fazer essa questão e entender bem a matéria, afinal estamos nos exercícios de fixação.
Mas aqui vai a dica para esse tipo de questão
![]()
Podíamos simplesmente fazer
Porque ele é simétrico, mas é importante fazer essas contas para ficar craque em centro de massa. Vamos continuar a questão.
Passo 9
Vamos agora achar ao longo do eixo
Sabemos que
Colocando o que der para colocar em evidência
Passo 10
Vamos escrever a posição do centro de massa na forma vetorial.