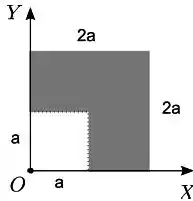
Uma chapa homogênea quadrada de lado tem um canto quadrado de lado retirado. A chapa restante está disposta no plano como indicado na figura. Em relação à origem , o vetor posição do centro de massa
Passo 1
Tínhamos uma chapa quadrada de lado e então tiramos um pedaço quadrado de lado da chapa. Ou seja, temos uma chapa com furo, assim podemos calcular a posição do centro de massa da figura pela fórmula
Lembre-se também que quando temos chapas usamos sua área no lugar da massa.
Passo 2
Vamos ter as posições do centro de massa
Além disso, temos as áreas
A área do buraco é negativa, pois é um buraco, estamos representando a ausência de área na figura.
Passo 3
Pela fórmula do centro de massa vamos ter
O vetor posição do centro de massa vai ser
Resposta
Letra