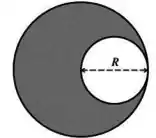
Uma massa de pizza perfeitamente circular e homogênea tem raio e massa. Se retirarmos dela pedaço perfeitamente circular com diâmetro de modo que a massa que resta tem a forma da figura, podemos afirmar que o centro de massa do que restou:
- Se deslocou uma distância para a esquerda do centro de massa original.
- Se deslocou uma distância para a direita do centro de massa original.
- Se deslocou uma distância para a esquerda do centro de massa original.
- Se deslocou uma distância R/2 para a direita do centro de massa original.
- Está na mesma posição do centro de massa original.
Passo 1
Bom galera, o primeiro passo pra entender isso, é notar que:
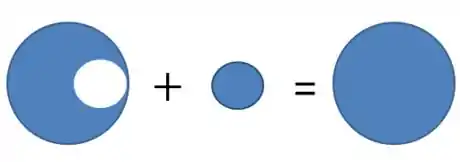
Legal? Guarda isso ai, e lembre-se que queremos calcular o centro de massa da primeira figura.
Mas vamos escrever isso matematicamente.
Passo 2
Bom, a ideia é que a posição do centro de massa da primeira massa mais a posição do centro de massa da segunda massa, a bolinha, é igual ao centro da esferona.
Bom, vamos estabelecer um eixo com a origem no centro da esfera completa. Mais ou menos assim:
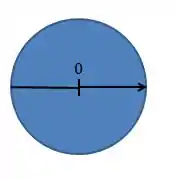
Assim, o centro de massa da massa maior é:
Beleza? Agora vamos tirar proveito da informação que o enunciado dá ao dizer que a massa de pizza é homogênea pra calcular a relação entre as massas.
Bom, a densidade da massa é constante, então:
Onde é a área da massa. Assim, a massa completa, o terceiro circulo da nossa equação de desenhos, é dada por:
E a massa da massinha é dada por:
Então:
Além do mais, a massa que tem um buraco, a que a gente quer calcular o centro de massa, é:
Show?
Vamos continuar.
Passo 3
Bom, então podemos escrever a equação do centro de massa da massa completa como a média ponderada entre a massa que tem um buraco e a massa pequena:
Show? Então, como isso é igual a zero:
Nós queremos achar . Porém, nós sabemos que o centro da outra massa é:
Assim:
Beleza? Como está negativo, quer dizer que o centro de massa se deslocou pra esquerda(de acordo com o eixo que adotamos).
Então:
a)
Resposta
a)