Considere dada por
- Determine a série de Fourier em cossenos de .
- Seja a soma da série de cossenos de , esboce seu gráfico em .
- Sendo definida no item anterior, qual o valor de ?
Passo 1
Beleza, vamos começar com a letra (a). Como o problema pede a série de Fourier em cossenos, então ele quer que façamos a extensão par desta função . Vamos chamar esta extensão de . Como é a extensão par, então precisamos que
Assim, vamos ter:
Uma vez que . E também:
Já que
Beleza. Feito isso, vamos considerar a periodicidade. Como definimos as expressões para o intervalo , então teremos que é períodica.
Show, então vamos determinar a série de Fourier em cossenos a partir disso agora. Ele pediu a série de Fourier em cossenos, vamos lembrar das nossa fórmulas:
Onde nesse caso. Começamos com :
Como a extensão é par, então podemos fazer
E esse vai ser nosso :
Um já foi, vamos agora para o :
Show, como a extensão é par e o cosseno é uma função par, então o integrando dado pelo produto das duas também será par, assim:
Para resolver essa integral, vamos usar integração por partes. Usando o LIATE, teremos
Portanto, vamos ter:
Teremos que para todo e .
Assim, nossa vai ficar:
Para poder escrever isso na série, para valores ímpares, definimos
Aí vamos ter:
Como
Então, vamos ficar com:
Fazendo a mesma coisa para par, vamos definir:
Aí teremos
Aí, depois desta conta toda, vemos que teremos referente aos teremos ímpares. Substituindo na fórmula da série em cossenos, vai ficar:
Passo 2
A letra (a) tardou, mas foi. Vamos agora para a letra (b) que vai sair mais naturalmente. Vimos que a expansão par é dada pela expressão
Aí, basta colocarmos no gráfico agora. Começamos com :
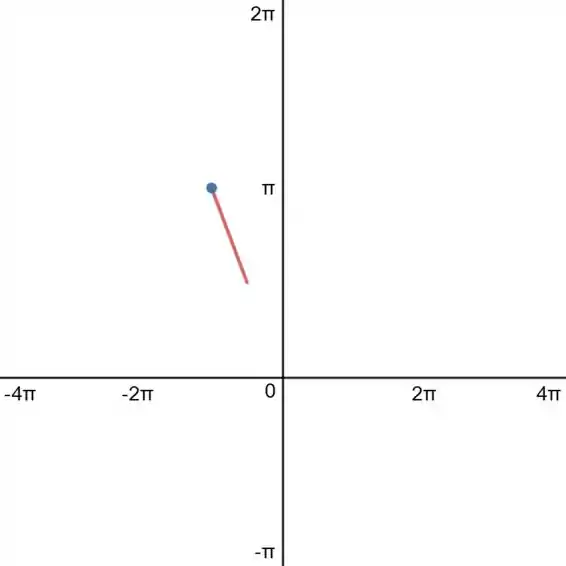
Agora, vamos para o intervalo em que a função vale zero:
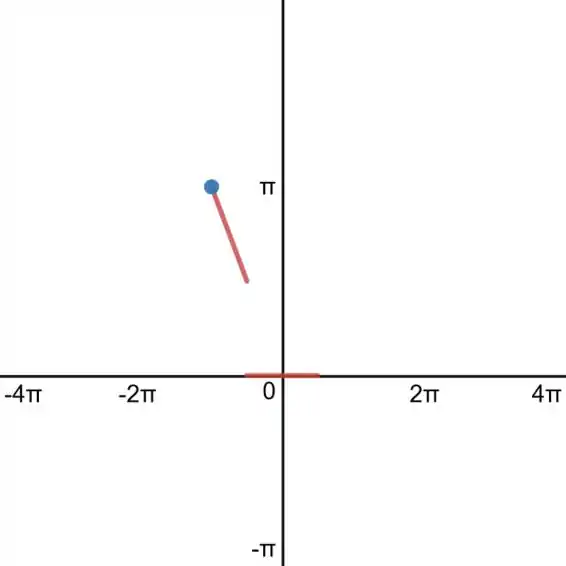
Agora, o intervalo em que tem expressão :
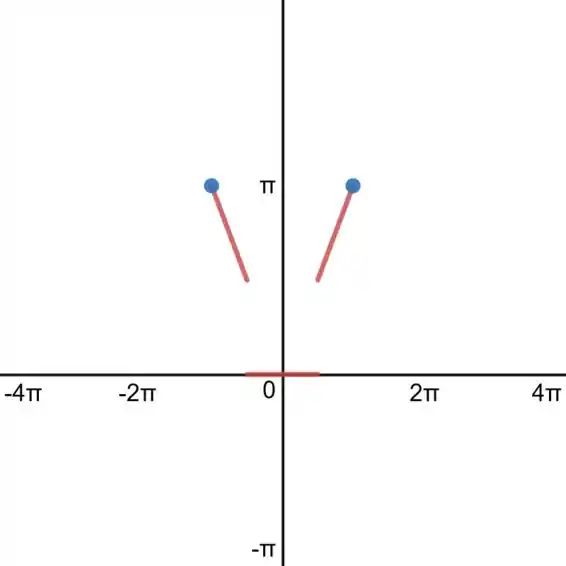
Agora, com a função é periódica, repetimos o gráfico até completar o intervalo que foi pedido:
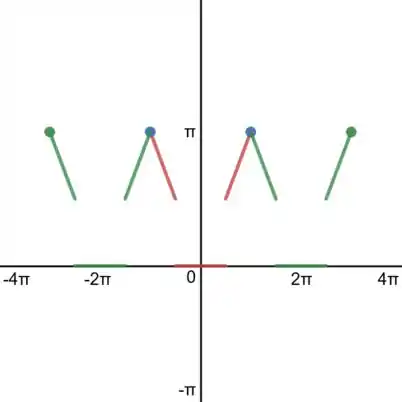
Acabou? Não! Ficarão faltando os pontos de descontinuidade que estão nestes saltos aí. Pelo teorema da série de Fourier, a série vai convergir para o valor médio da função no ponto de descontinuidade.
Então vamos pegar um ponto de descontinuidade que pode ser na troca da expressão de para em . Assim, vamos ter:
Al��m disso, olhando para o gráfico, todos os pontos de descontinuidade terão esse valor e fechamos o esboço marcando-os: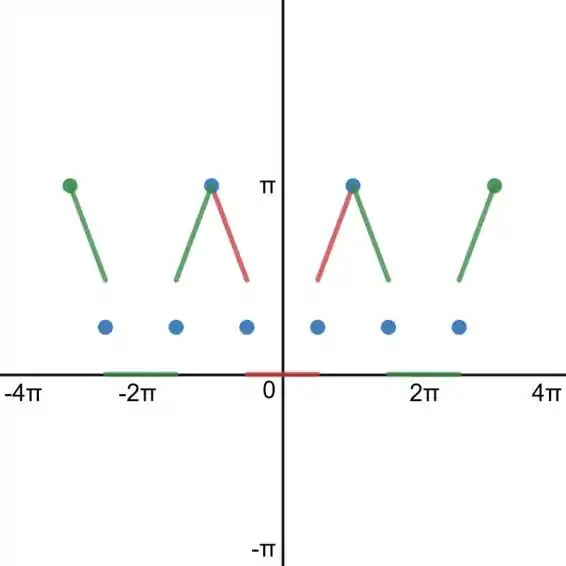
Passo 3
Agora vamos para a letra (c), teremos que, pela série de Fourier da extensão:
Como a função é periódica:
E lá do gráfico da (b) na descontinuidade, teremos:
Resposta
a)
b)
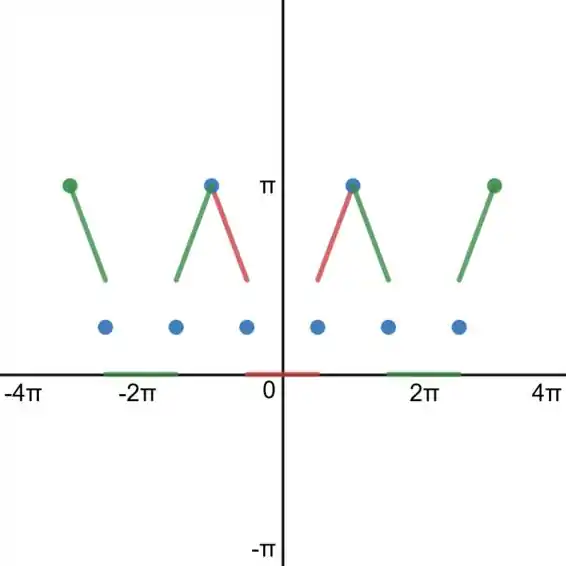
c)