Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Série de Fourier apenas em senos ou cossenos

Ver Teoria
Exercício 281234567891011121314151617181920212223242526272930313233343536373839404142434445464748495051525354555657

Enunciado

Seja f x = e x - 2 ,     x ∈ ( 0 , π ] .

( a ) Determine a série de senos de f .

( b ) Encontre a soma S ( x ) da série de senos de f e esboce o seu gráfico no intervalo [ - 3 π , 3 π ] .

c Determine S 2117 π 2

Passo 1

Só pra lembrar que a série de Fourier é a seguinte:

f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n π x L + ∑ n = 1 ∞ b n sen ⁡ n π x L

Como queremos a série de senos, temos:

f x = ∑ n = 1 ∞ b n sen ⁡ n π x L

e x - 2 = ∑ n = 1 ∞ b n sen ⁡ n π x π

b n = 2 π ∫ 0 π e x - 2 sen ⁡ n x d x

b n = 2 π ∫ 0 π e x sen ⁡ n x d x - 2 ∫ 0 π sen ⁡ n x d x

Passo 2

Vamos começar resolvendo esta integral:

∫ 0 π e x sen ⁡ n x d x

Faremos a integração por partes. Lembra da fórmula?

∫ u d v = u v - ∫ v d u

Chamando d v = e x d x → v = e x ; u = sen ⁡ n x → d u = n cos ⁡ ( n x ) :

∫ 0 π e x sen ⁡ n x d x = e x sen ⁡ n x 0 π - n ∫ 0 π e x cos ⁡ n x d x

Passo 3

Novamente, vamos resolver com integração por partes a integral:

∫ 0 π e x cos ⁡ n x d x

Chamando d v = e x d x → v = e x ; u = cos ⁡ n x → d u = - n sen ⁡ ( n x ) :

∫ 0 π e x cos ⁡ n x d x = e x cos ⁡ n x 0 π + n ∫ 0 π e x sen ⁡ n x d x

Colocando de volta naquela equação:

∫ 0 π e x sen ⁡ n x d x = e x sen ⁡ n x 0 π - n e x cos ⁡ n x 0 π + n ∫ 0 π e x sen ⁡ n x d x

∫ 0 π e x sen ⁡ n x d x = e x sen ⁡ n x 0 π - n e x cos ⁡ n x 0 π - n 2 ∫ 0 π e x sen ⁡ n x d x

1 + n 2 ∫ 0 π e x sen ⁡ n x d x = - n e x cos ⁡ n x 0 π

∫ 0 π e x sen ⁡ n x d x = - n e x cos ⁡ n x 0 π n 2 + 1 = - n e π cos ⁡ n π - 1 n 2 + 1 = n ( 1 + - 1 n + 1 e π ) n 2 + 1

Passo 4

Assim, nosso b n vai ser:

b n = 2 π n ( 1 + - 1 n + 1 e π ) n 2 + 1 - 2 ∫ 0 π sen ⁡ n x d x

b n = 2 π n 1 + - 1 n + 1 e π n 2 + 1 + 2 cos ⁡ n x n 0 π

b n = 2 π n 1 + - 1 n + 1 e π n 2 + 1 + 2 cos ⁡ n π n - 1 n

b n = 2 π n ( 1 + - 1 n + 1 e π ) n 2 + 1 + 2 n - 1 n - 1

AEEE!

f x = ∑ n = 1 ∞ 2 π n 1 + - 1 n + 1 e π n 2 + 1 + 2 n - 1 n - 1 sen ⁡ n x

Passo 5

b Encontre a soma S ( x ) da série de senos de f e esboce o seu gráfico no intervalo [ - 3 π , 3 π ] .

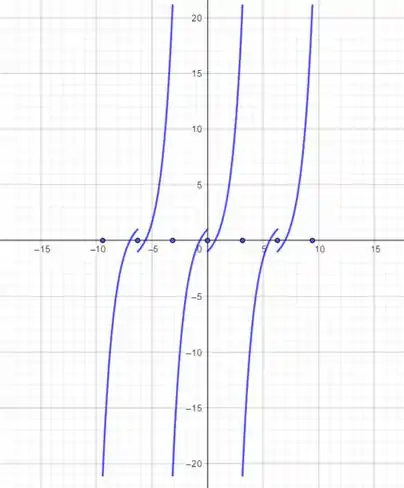
Vamos começar com a noção intuitiva do gráfico, depois nós provaremos matematicamente ok? Começamos desenhando nossa função no intervalo dado:

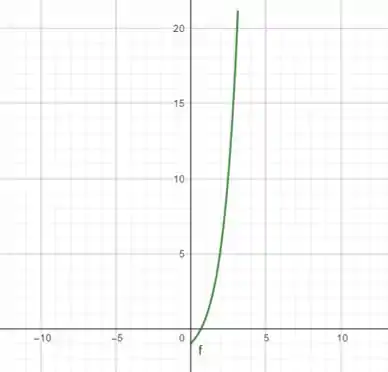
Agora vamos refletir no eixo y :

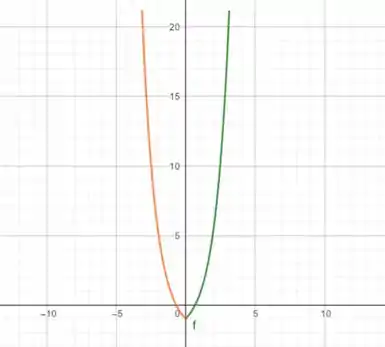
Agora refletimos no eixo x e não se esqueça de que os pontos de descontinuidade serão as médias dos valores da função naqueles pontos.

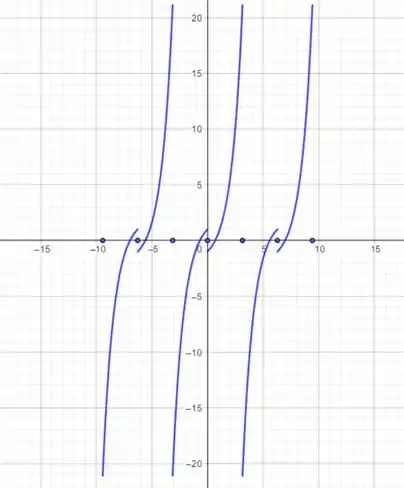
Pronto. Ficou lindo! Agora vamos fazer isso matematicamente! Vamos chamar de S x essa expansão. Nossa função ímpar tem que obedecer:

S - x = - S x

Então vamos ficar com:

S x = e x - 2 ,     s e   0 < x < π 2 - e - x ,     s e - π < x < 0 0 ,     s e   x = 0 ; ± π

Agora é só repetir isso aí periodicamente:

S x = S x + 2 k π ,   ∀ x ∈ R ,   ∀ k ∈ Z

Passo 6

c Determine S 2117 π 2

Bom, a gente sabe que nossa função é periódica a cada 2 π . Então vamos tentar escrever esse número 2117 π 2 com fatores de 2 π , desse jeito:

2117 π 2 = 529 2 π + π 2

No fundo é só dividir e olhar o resto 😊

S 2117 π 2 = S 529 2 π + π 2 = S π 2 = f π 2 = e π 2 - 2

Resposta

a f x = ∑ n = 1 ∞ 2 π n 1 + - 1 n + 1 e π n 2 + 1 + 2 n - 1 n - 1 sen ⁡ n x

( b )

S x = e x - 2 ,     s e   0 < x < π 2 - e - x ,     s e - π < x < 0 0 ,     s e   x = 0 ; ± π

S x = S x + 2 k π ,   ∀ x ∈ R ,   ∀ k ∈ Z

( c ) S 2117 π 2 = f π 2 = e π 2 - 2

Exercícios de Livros Relacionados

(a) Sejam v 1 ,v 2 e v 3 três vetores ortogonais dois a dois em três dimensões, e seja u qualquer vetor tridimensional. Mostre que u = a 1 v 1 + a 2 v 2 + a 3 v 3 , Em que a i = u ∙ v i v i ∙ v i , i
f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função
Considere a função f definida no problema 21, e seja e m = f x - s m ( x ) . f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 2 para diversos valores
f x = x ,- 1 ≤ x1 f x + 2 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função de
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. x 2