Encontre a série de Fourier da (i.e da extensão par e periódica de período da função
Esboce o gráfico da .
Passo 1
Então pessoal, vamos começar desenhando essa função normalmente:
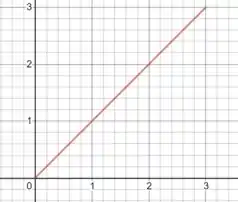
A ideia da extensão par é a seguinte: a gente vai prolongar essa função para um período , de forma que ela obedeça:
Ou seja, é só refletir a função no eixo :
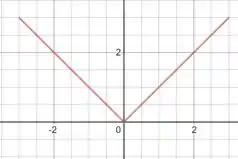
E aí podemos escrever essa nova função desse jeito:
Nosso objetivo é achar a série de Fourier dessa função aí.
Passo 2
Como estamos falando de uma função par, vamos ver como ficam as fórmulas para a série de Fourier. Primeiro, a forma geral da função:
O coeficiente é:
E os coeficientes são:
E no nosso caso, como o próprio enunciado já disse:
Então beleza, vamos aplicar essas fórmulas.
Passo 3
O primeiro passo é calcular a constante :
Substituindo :
E nesse intervalo, a função é definida simplesmente como , então:
Como a integral de :
Passo 4
E o próximo passo é encontrar a fórmula para os coeficientes :
Substituindo de novo e :
O jeito mais fácil de resolver essa integral, é olhando pra integral indefinida primeiro:
Onde esse é uma constante qualquer, que no nosso caso vai virar o . Vamos usar integração por partes. A fórmula é essa aqui:
E agora a gente tem que escolher quem chamar de e quem chamar de .
O nosso ali do lado direito é simplesmente a integral de em relação a .
Substituindo isso na fórmula:
E a integral de é , então:
Beleza, agora a gente tem uma fórmula pra resolver aquela integral.
Passo 5
Então tá, vamos aplicar essa fórmula. Queremos resolver essa integral aqui:
E a nossa fórmula diz que:
No nosso caso, . Vamos calcular nos dois limites de integração, começando por :
Mas e , então:
E como e :
Agora é só subtrair uma da outra:
Reorganizando um pouco:
Passo 6
Vamos dar uma olhada nesse termo aí entre parênteses:
Olha o que acontece quando é par/ímpar:
Ou seja, se a gente montar a nossa série desse jeito aqui:
Só substituindo , e :
Todos os termos com par vão se anular pelo que a gente viu ali em cima, então só sobram os termos ímpares,.
Então vamos fazer (com começando em ) e :
Simplificando um pouco:
Pronto! Essa é a série de Fourier da extensão par da função.
Resposta
A série de Fourier da extensão par da função é .