Seja
b) Estenda para todos os outros valores reais de como uma função ímpar e periódica de período . Esboce o gráfico da extensão.
c) Calcule a série de Fourier da extensão ímpar de .
Passo 1
b)
Igual o que fizemos na primeira letra, vamos primeiro lembrar a formula para estender como função impar.
A ideia do período vai ser a mesma, então A nossa função será
Passo 2
Esboçando esse gráfico teremos.
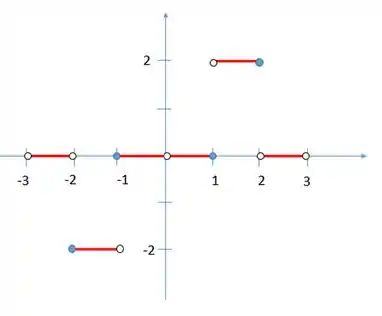
Passo 3
c)
Vamos lembrar que quando calculamos a série de Fourier de uma função impar nós acabamos com uma série só de senos. Não precisamos calcular os coeficientes para os cossenos e a nossa série de Fourier será.
Onde
Vamos partir pros cálculos agora.
Passo 4
Calculando
Assim a nossa série será.
Resposta
- b)
- b)
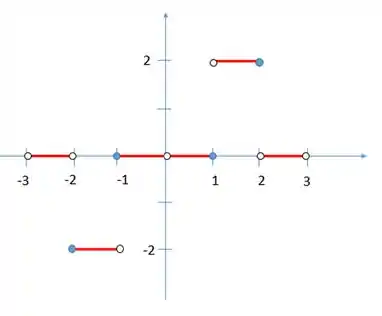
- c)
Exercícios de Livros Relacionados
(a) Sejam v 1 ,v 2 e v 3 três vetores ortogonais dois a dois em três dimensões, e seja u qualquer vetor tridimensional. Mostre que u = a 1 v 1 + a 2 v 2 + a 3 v 3 , Em que a i = u ∙ v i v i ∙ v i , i
f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função
Considere a função f definida no problema 21, e seja e m = f x - s m ( x ) . f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 2 para diversos valores
f x = x ,- 1 ≤ x1 f x + 2 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função de
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. x 2