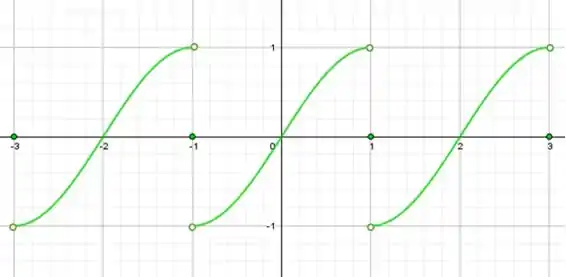
Seja para .
Calcule a série de Fourier em senos da função .
Esboce o gráfico da série de Fourier obtida no item no intervalo .
Calcule o valor limite da série
Passo 1
Vamos lembrar nossas fórmulas pras séries de Fourier em senos, fera!
No nosso caso, !
Passo 2
Vamos começar achando substituindo as coisas na fórmula:
Lembrando da seguinte propriedade:
Subtraindo uma da outra:
Repara agora que podemos substituir aquele produto de senos na integral por essa relação aqui em cima:
Passo 3
Resolvendo a integral agora:
Aqui vamos usar o seno da soma:
Maneiro! Mas agora podemos escrever o cosseno em função de , dessa maneira:
Então, de forma geral:
Logo,
Passo 4
Juntando as duas:
Então nossa função fica:
Passo 5
Esboce o gráfico da série de Fourier obtida no item no intervalo
Para esboçar o gráfico dessa função vamos ter que a expandir. E não podemos nos esquecer de que tem que ser uma expansão ímpar pra ficarmos com uma série de Fourier em senos! Todo esse desenvolvimento da letra foi feito assumindo uma expansão ímpar de 😉
Vamos começar com a noção intuitiva do gráfico e depois faremos matematicamente. Bora começar desenhando nossa :
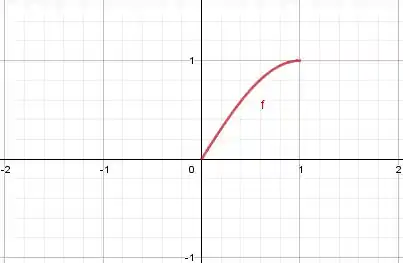
Agora a gente reflete no eixo :
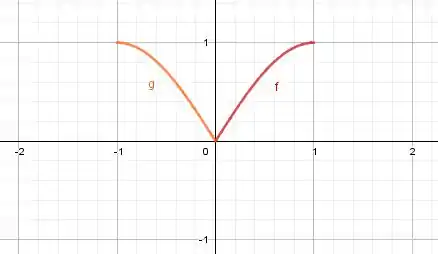
E finalmente, a gente reflete no eixo , isso nos dá a extensão ímpar da função:
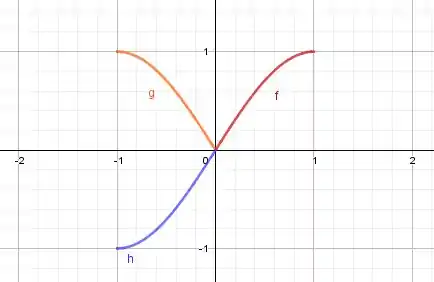
E a parte que nos interessa é a união da linha azul com a vermelha, que eu vou colorir de verde, ok?
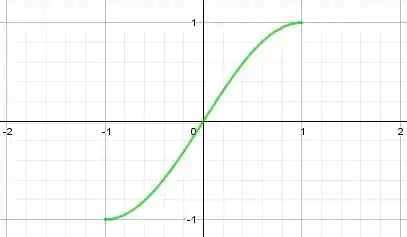
Legal! Agora faremos isso matematicamente. Vamos chamar de essa expansão. Nossa função ímpar tem que obedecer:
Então vamos ficar com:
Agora é só repetir isso aí periodicamente:
Outra coisa importante pra lembrar é que essa é a extensão ímpar da nossa , mas o que a letra está pedindo é o gráfico da série de Fourier! A única diferença é que, nos pontos de descontinuidade vamos ter que tirar a média! Assim olha:
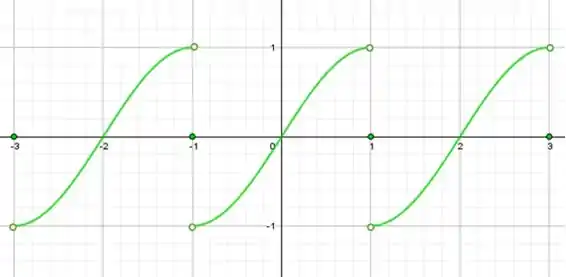
Passo 6
Calcule o valor limite da série
Vou logo avisando pra se preparar porque essa letra não é muito bonita não haha.
Bom, certamente nós vamos ter que usar aquela série de Fourier da letra pra alguma coisa né? Então vamos jogar ela aqui:
Agora você tinha que ter uma iluminação divina de pensar em usar o ponto ! Ué, mas por que ? Porque assim aparece o termo que sabemos ser quando é par! Pois é! Ficaria assim:
Lembrando que:
Para temos:
Com isso, a gente pode desconsiderar os pares e pegar só os ímpares pela mudança :
Repare que temos:
Show?
Ta ficando parecido com o que a letra pede, hein! Vamos dar uma mexida agora naquele que ta diferente:
Po, mas elevado à um número par é sempre ! Então:
Agora a gente desenvolve esse seno:
Agora você tinha que buscar lá do fundo do baú das lembranças que ! Aí ficamos com:
E agora repara que se for par, o cosseno vale e se for ímpar, o cosseno vale ! Então:
Substituindo:
Aeeeeee!!!! Finalmente encontramos!
Resposta