Seja
a) Estenda para todos os outros valores reais de como uma função par e periódica de período . Esboce o gráfico da extensão.
Passo 1
Para estendermos essa função, vamos primeiro lembrar a fórmula para estender como uma função par.
Lembrando que será o período, teremos . Nossa função expandida será.
Passo 2
Esboçando esse gráfico teremos.
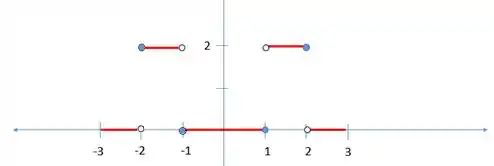
Resposta
a)