Séries de Fourier, Funções pares e ímpares e desigualdade de bessel e identidade de Parseval
Seja
a) Determine a série de Fourier de senos de
b) Obtenha a soma da série de Fourier de senos de , e esboce o gráfico de no intervalo
c) Determine
Passo 1
a)
Quando ele pedir a série de Fourier a primeira coisa que sempre vamos fazer é o gráfico. Então vamos fazer gráfico da
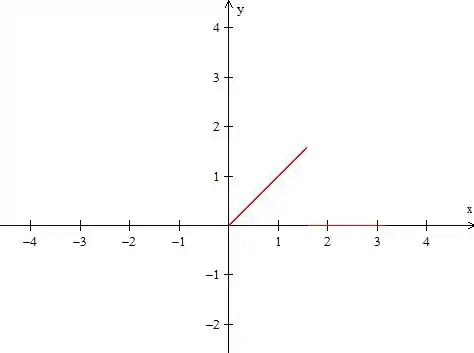
Repara que ele pediu uma série de Senos, para termos uma série de Senos precisamos de uma função ímpar. Essa função por enquanto não é nem par nem ímpar. Precisamos da sua extensão ímpar. Para isso, vamos começar espelhando essa função em relação ao eixo
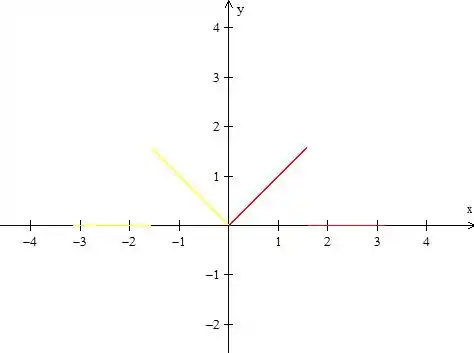
Essa parte amarela é a parte espelhada. Agora precisamos espelhar essa parte amarela em relação ao eixo .
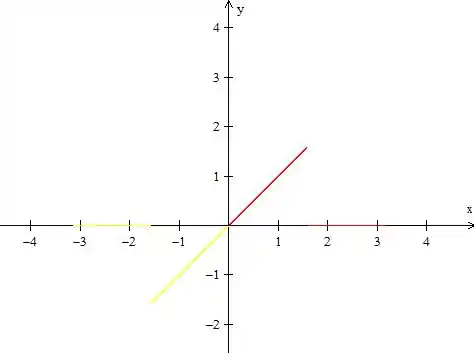
O período de vai ser então, a função vermelha mais a função amarela. Então para desenharmos a função só precisamos repetir isso ao longo da parte toda. Além disso, vamos colocar os períodos marcados por retas tracejadas só para deixar bem indicado a parte da função que se repete.
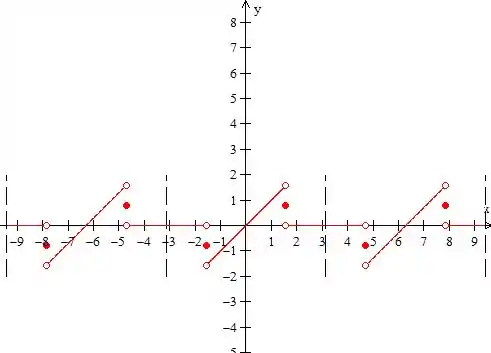
Repara nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de salto, a função vale a média dos limites laterais.
Com temos
Com
Assim temos que colocar, bola cheia no valor que está na metade do salto, e bola vazia nos “extremos” do salto.
Passo 2
Beleza, agora que temos o gráfico vamos para a série de Fourier.
A primeira coisa que temos que descobrir para fazer a série de Fourier é o período. Olhando aquele gráfico que fizemos podemos descobrir o período da extensão ímpar. O período ali do meio vai de até , isso nos diz que
Agora, repara que temos a série de senos da extensão ímpar, assim
Como vimos, o período vai ser , assim
Passo 3
Vamso calcular os valores de . Temos que
Trocando o valor de nessa integral, vamos ter de à sendo e no resto sendo . Então
Precisamos resolver essa integral, para isso vamos fazer integração por partes
Pegando
A nossa integral vai ficar
Voltando para nossa integral
Passo 4
Agora que temos o valor de , bata substituirmos na fórmula de ali do passo
Passo 5
b)
Aqui ele quer a fórmula da série de Fourier e o seu gráfico. O gráfico já fizemos no passo
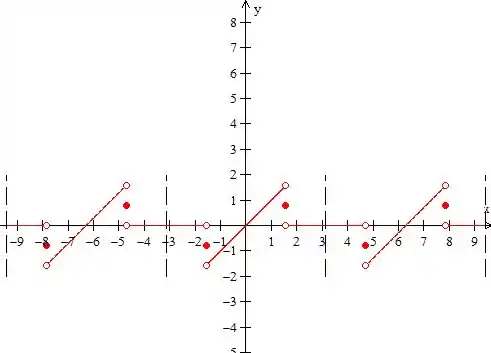
Vamos escrever a fórmula agora, primeiro só na parte entre e .
Entre e , temos a fórmula . Na outra parte do intervalo temos . E nos pontos de “pulo” temos
Assim nossa função vai ser
Agora vamos escrever a soma , que vai ser essa extendida para qualquer valor de .
Repara que se somarmos no valor de , o valor da função em não muda,
Então podemos pegar cada pedaço de intervalo ali e somar no extremos, ou nos pontos. Podemos fazer isso para qualquer múltiplo natural de . Além disso, podemos subtrair também qualquer múltiplo natural de , assim a nossa função tem essa cara
Onde é um inteiro, isso porque ele pode ser qualquer natural positivo ou negativo.
A soma no intervalo de até vai ser a própria . Assim
Agora é só pegar a nossa e comar nos intervalos o
Passo 6
c)
Agora precisamos achar
Para isso precisamos descobrir em que intervalo esse cara está naquela fórmula da que achamos no passo anterior. Para isso temos que ir subtraindo o período do valor de que ele quer até chegarmos em um valor entre e .
Vamos fazer isso na mão assim? Eu me assusto em pensar em ir tirando em , mo doidera isso, vai que fico aqui até amanha fazendo isso. Vamos ver qual o valor que está multiplicando o , fazendo a divisão entre e
Temos que comparar esse valor com os possíveis intervalos de que ele vai estar. Repara que ele precisa necessariamente igual a um dos intervalos onde temos ou somados com . Isso porque ele é um inteiro mais uma metade, , sacou?
Isso nos diz que temos que fazer
Ou
Uma dessas duas equações vai nos dar o valor certo de , enquanto a outra não vai dar.
Vamos resolver as duas e ver qual delas vai dar um problema.
Como é um cara inteiro ele não pode ser .
Assim temos que
E isso nos diz que o valor da soma em é o mesmo do valor da soma em . Coisa de função periódica isso rs
Resposta
a)
b)
c)