Considere a função , .
- Determine uma série de Fourier em senos para a função .
- Esboce o gráfico da função para a qual a série de Fourier obtida no item (a) converge no intervalo . Justifique sua resposta.
Passo 1
Letra b)
A letra é a que pede o gráfico da série de Fourier, mas vamos fazer logo aqui porque isso ajuda muito para visualizar a questão, ok? Vamos lá. Graficamente é isso aqui:
Essa é a definição de que o problema deu de a :
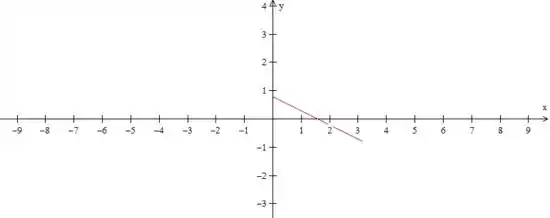
Para desenhar essa reta, você tem que achar os valores de e .
Vamos fazer a extensão ímpar dessa função, porque o problema pede uma série de senos. Primeiro nós espelhamos ela em relação ao eixo
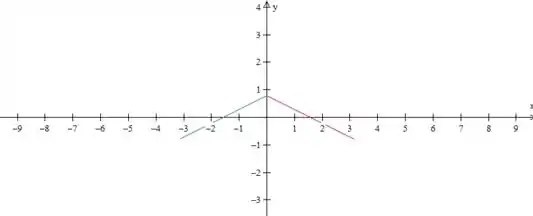
Espelhamos essa reta verde no eixo :
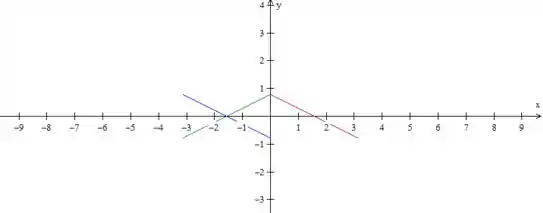
O período de é então essa parte azul mais a vermelha, para termos uma função em série de senos temos que ter ímpar como já vimos, para isso devemos pegar a função entre e , fazendo essa marotagem que fizemos ali de espelhar no eixo e depois no eixo , isso garante que nossa função seja ímpar, mas para isso tudo dar certo temos que pegar de à fazendo o período ser
! É só repetir isso aí.
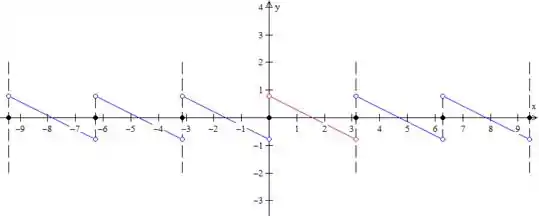
Pronto, temos então a função periódica. É bom você sempre desenhar esse tracejado grande para marcar o período da função, para não se perder!
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de salto, a função vale a média dos limites laterais. Nesse caso:
Nós colocamos então as bolinhas cheias em (repare que todas as retas tem bolinhas vazias nas suas extremidades). Não poderia ser diferente, né? Uma extensão periódica ímpar sempre apresenta:
Como a gente já viu. Isso é muito importante! Não se esqueça!
Passo 2
Letra a)
Beleza, agora vamos montar o problema. Como a função é ímpar, temos o seguinte:
Como o período da função é , temos:
Passo 3
Vamos calcular os ’s. Temos que:
Agora vamos substituir a expressão de :
Agora vamos fazer a integração por partes:
Lembrando que
Podemos escrever
Passo 4
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá