Seja a função definida por
- Determine a série de Fourier em cossenos de
- Esboce o gráfico da série de Fourier obtida no item (a) no intervalo [0,6]
- Calcule o valor da série
Passo 1
a)
Ele pediu a série de Fourier em cossenos, vamos lembrar das nossa fórmulas
Onde nesse caso.
Passo 2
Vamos calcular os coeficientes
Para
Calculando essa integral
Agora que obtemos os coeficientes temos que a série será
Passo 3
b)
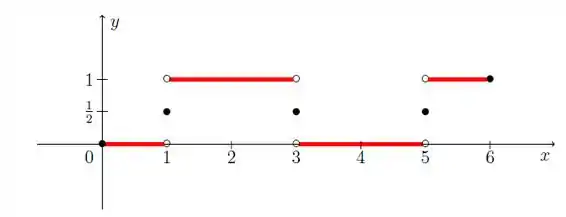
Para esboçar o gráfico dessa função no intervalo [0,6] vamos ter que expandi-la.
Temos que definir um valor novo para o ponto de descontinuidade de forma que
Assim t eremos o gráfico abaixo.
Passo 4
c)
Como a extensão par de é continua em podemos dizer, pelo Teorema de Convergência de Fourier que
Disso obtemos que
Beleza, isso tudo é muito legal, mas não fizemos isso à toa. Vamos analisar os valores de
Agora está começando a aparecer o que estamos procurando. Percebemos que daquele nosso somatório nós só teremos valores diferentes de zero quando for impar. Então podemos escrever
Resposta
a)
b)
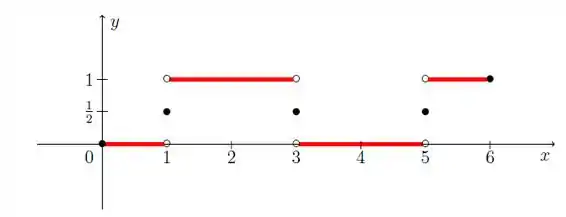
c)