Seja
- Estenda como função ímpar periódica de período para .
- Faça o gráfico de estendida no intervalo .
- Encontre a série de Fourier de . Justifique a convergência da série de Fourier.
- Faça o gráfico da função para a qual a série de Fourier converge no intervalo .
Passo 1
Letra b)
Vamos começar fazendo o gráfico da função estendida, para a gente poder visualizar melhor a questão, ok? Primeiro, vamos desenhar os dados do enunciado:
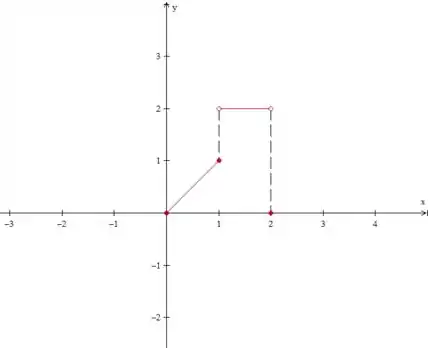
O próximo passo é espelhar isso que desenhamos do eixo , dessa forma:
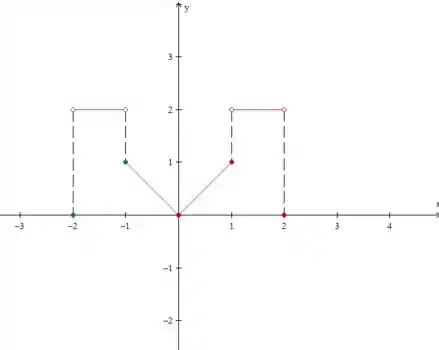
Cuidado com os pontos de descontinuidade! Temos que levar eles junto.
Beleza, mas isso ai seria uma extensão par, não é? Pra fazermos uma extensão ímpar temos que rebater essa parte azul no eixo , ou seja, jogar ela para baixo:
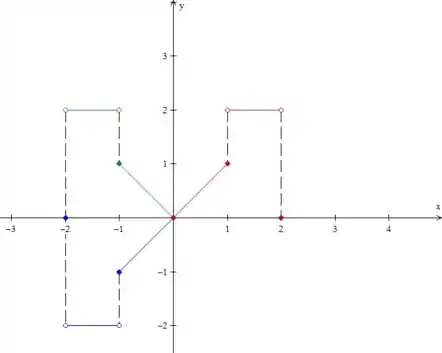
Certo, o período da função que queremos é então essa parte azul mais a vermelha! Como esse é o padrão que se repete, vamos copiá-lo para a direita, olha só:
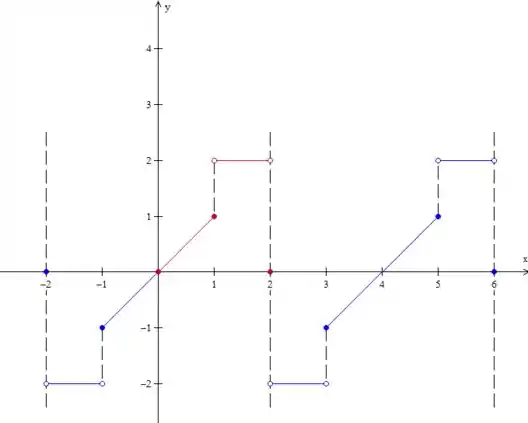
Pronto, temos então a função estendida no intervalo de a , como pede o enunciado. É bom você sempre desenhar esse tracejado grande para marcar o período da função, para não se perder!
Mais uma vez, lembre-se de levar os pontos de descontinuidade junto nesse passo a passo, ok?
Passo 2
Letra a)
Agora vamos fazer essa extensão matematicamente.
A definição de uma função ímpar diz que
Escrevemos porque estamos falando da extensão de , ok? Como a extensão tem período , podemos dizer que:
Beleza, vamos fazer isso aí. Como o período é , precisamos definir a função em e repetir esse padrão. Está faltando a definição de entre e .
Para :
Essa é a equação da parte vermelha.
Para :
Essa é a equação da parte azul. Se você se confundir com a definição de função ímpar, dá uma olhada no gráfico. Nesse caso, é até mais fácil.
Não podemos nos esquecer de que na origem e em a função deve valer zero em uma extensão ímpar, então está tudo certo aqui.
Temos portanto a seguinte extensão:
Como a função é periódica, isso se repete
Passo 3
Letra c)
Beleza, agora vamos encontrar a série de Fourier. Como a função é ímpar, temos o seguinte:
Como o período da função é como o enunciado pediu, temos:
Passo 4
Vamos calcular os ’s. Temos que:
Como temos mais de uma expressão para em , precisamos dividir essa integral:
Agora vamos fazer a integração por partes:
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Passo 6
Letra d)
Beleza, agora temos que desenhar o gráfico da função para a qual a série de Fourier converge. Peraí, nós já não fizemos isso? Mais ou menos!
Lembra do Teorema da Convergência de Fourier? Não? Sem problemas, ele dizia o seguinte: a série de Fourier de uma função converge para onde essa função é contínua e, nos seus pontos de salto, converge para a média dos limites laterais.
Calma, vamos explicar! Esse é o gráfico da função:
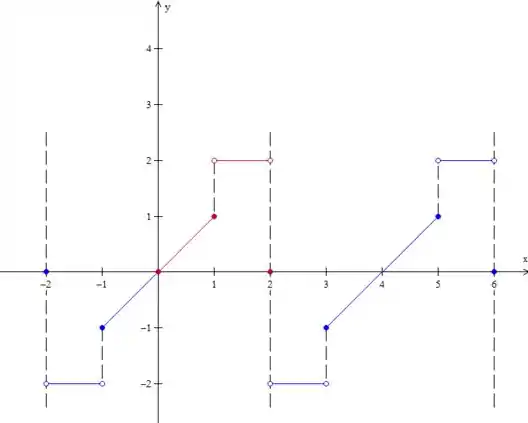
Tá vendo as retas? Nesses pontos a função é contínua e a sua série converge exatamente para essas retas que representam , então nós vamos copiar as retas iguaizinhas.
Agora olha os pontos em que ela muda de definição, onde temos saltos (). Nesses pontos, a soma da série não vai ser igual à função, portanto, podemos ignorar essas bolinhas cheias e vazias!
Para esses pontos, a série converge para a média dos limites laterais, então precisamos calcular esses valores.
Só precisamos então desenhar esses pontos no gráfico e repetir o padrão.
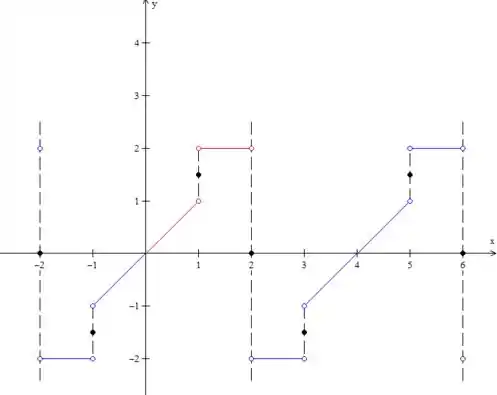
Percebeu a diferença? Marcamos em preto nos novos valores nas descontinuidades.