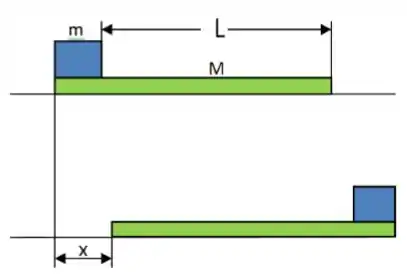
Um bloco de massa está apoiado sobre o lado esquerdo de um bloco de massa . O coeficiente de atrito cinético entre os dois blocos é de 0,3 e a superfície sobre a qual o bloco de está apoiado é sem atrito. Uma força horizontal constante de módulo é aplicada ao bloco de , colocando-o em movimento como mostrado na figura abaixo. Se a distância que a superfície frontal do bloco menor percorre sobre o bloco maior é de .
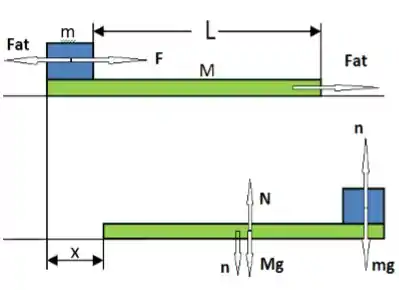
a) Desenhe todas as forças que atuam no sistema
b) Calcule a aceleração do bloco menor em relação ao solo
c) Calcule a aceleração do bloco maior em relação ao solo
d) Qual a distância percorrida pelo bloco maior e quanto tempo o bloco menor levará até chegar ao lado direito do bloco maior?
Passo 1
(a)
Passo 2
(b)
A aceleração do bloco menor pode ser calculada usando a segunda lei de Newton, ou seja:
Lembrando que e que, nesse caso,
Passo 3
(c)
Da mesma forma, aplicando a segunda lei de Newton, obtemos que:
Passo 4
(d)
Vamos escrever a equação de movimento para os dois blocos:
Bloco menor:
Bloco maior:
Dividindo uma equação pela outra obtemos:
Substituindo o valor de na segunda equação obtemos que:
Resposta
(a)
(b)
(c)
(d) ;