Dois blocos de massas e estão ligados por um fio de massa desprezível e repousam sobre um plano inclinado que forma um ângulo com a direção horizontal. O bloco é empurrado por uma força constante de módulo que faz um ângulo com a direção do plano inclinado, (veja a figura) e o conjunto entra em movimento. O coeficiente de atrito cinético entre os blocos e a superfície do plano inclinado é . Todas as respostas devem ser fornecidas em relação ao sistema de coordenadas mostrado na figura.
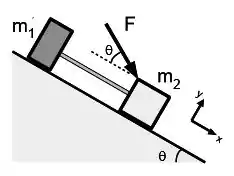
(a) Faça o diagrama do corpo livre, indicando claramente todas as forças que agem em cada um dos blocos. Indique as forças que formam par ação e reação.
(b) Escreva as equações do movimento na sua forma literal em termos das componentes das forças que agem sobre os blocos. Informe as expressões literais para as componentes da força e dos pesos dos blocos e .
Considere para os itens seguintes os seguintes valores: ; ; ; ; ; ; .
(c) Determine os módulos da aceleração dos blocos e da tensão no fio que liga os blocos.
(d) Considere agora que o sistema esteja na condição de repouso. Para que ele mantenha esta condição inercial, determine o menor valor do coeficiente de atrito estático entre os blocos e a superfície de apoio.
Passo 1
(a) Estes são os diagramas de corpo livre:
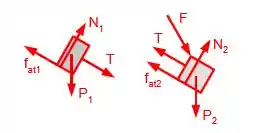
Diante dos diagramas mostrados, percebemos que não há pares ação-reação.
Passo 2
(b)
Bloco 1:
Bloco 2:
Componentes:
Passo 3
(c) Da equação :
Da equação :
Somando as equações e :
Substituindo o resultado da aceleração em equação :
Passo 4
(d) Como o sistema está em repouso, o atrito entre os blocos é estático e a aceleração dos blocos é nula. Para um mesmo valor de coeficiente de atrito estático, a força de atrito estático assume seu valor máximo para a situação em que o sistema está na iminência de se mover , relacionado ao menor valor de coeficiente de atrito que mantém o sistema parado, visto que se é aumentado o coeficiente de atrito estático, o sistema não estaria na iminência de se mover. Logo, pela soma das equações e :
Resposta
c)
d)