Força e Leis de Newton, Força de Atrito
Na figura, o fio e a roldana são ideais, e o plano fixo em que se apoia o bloco possui inclinação com a horizontal. Em todas as situações abaixo, o fio permanece tensionado e , mas o bloco pode variar. Quando necessário substituir valores, use .
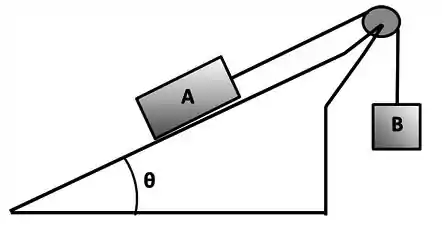
Neste item, considere e . Se o bloco adquire aceleração para baixo de , calcule o coeficiente de atrito cinético entre o plano e o bloco .
Passo 1
Estamos estamos considerando o atrito entre o bloco e o plano, a equação de movimento ficará um pouco diferente. Pelo fato de o bloco ter aceleração para baixo, teremos a força de atrito atuando no bloco na mesma direção e sentido da componente da sua força peso, ou seja, oposta ao movimento! A equação fica assim:
A equação de movimento do bloco não sofrerá alteração, será portanto:
Somando as duas equações, para eliminar a tração, temos:
Substituindo os valores, temos:
Resposta