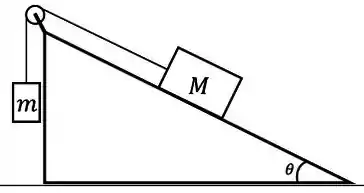
Considere a situação ilustrada na figura abaixo. Um bloco de massa está conectado através de fios e polias ideais a um segundo bloco de massa . O bloco de massa desliza com atrito sobre uma superfície inclinada de um ângulo com a horizontal enquanto o bloco de massa desce verticalmente com velocidade constante. Responda as perguntas a seguir: (Lembre-se que sua resposta deve ser dada em função dos dados fornecidos no problema: , , , )
a) Faça o diagrama das forças que atuam sobre cada um dos blocos.
b) Determine o módulo da força de atrito entre o bloco de massa M e o plano inclinado;
c) Encontre o coeficiente de atrito cinético entre o bloco de massa M e o plano inclinado.
Passo 1
Bom, temos o sistema da figura e na letra (a) já queremos o diagrama das forças sobre os blocos, sabendo que o bloco de massa está descendo e o bloco de massa está subindo a rampa.
Para o bloco de massa é tranquilo, pois temos apenas a força peso para baixo e a tração na direção do cabo (para cima):
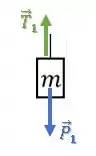
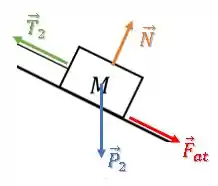
Já no segundo bloco, além da força peso para baixo , tração na direção do fio e a força normal perpendicular à superfície, temos também uma força de atrito para considerar.
A força de atrito atua contra a tendência de deslizamento, como esse bloco de massa está subindo, temos a força de atrito para baixo da rampa.
Passo 2
Na letra (b), queremos achar o valor (módulo) da força de atrito.
Para isso, vamos aplicar a Segunda Lei de Newton para os dois blocos e manipular as equações.
Para o bloco de massa , temos que se o bloco desce com velocidade constante, então a força resultante sobre ele é nula:
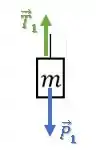
Já para o bloco de massa , vamos decompor a força peso e depois escrever a equação de forças para a direção paralela e perpendicular à rampa.
O ângulo aparece aqui:
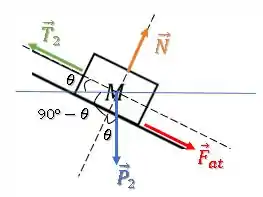
Então, as componentes da força peso são:
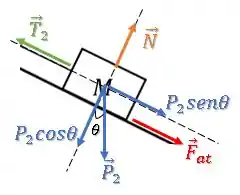
Na direção perpendicular à rampa, temos um equilíbrio de forças:
Já na direção paralela à rampa, temos também um equilíbrio de forças, pois se o bloco desce com velocidade constante, o bloco é puxado com uma velocidade constante.
Considerando o sentido positivo para cima:
Passo 3
Beleza, ficamos com essas equações:
Como o fio é ideal, a força de tração é a mesma por todo o cabo, então:
Que vamos chamar simplesmente de .
Então, nosso sistema ficou assim:
Passo 4
Agora, vamos encontrar uma expressão para a em função dos dados (, , , ).
Como não temos o valor da tração , vamos eliminar exatamente esse cara da expressão. Basta substituir o da primeira equação na terceira equação.
Substituindo na terceira equação:
Passo 5
Na letra (c), queremos o coeficiente de atrito cinético.
A força de atrito será cinética pois o bloco está deslizando, então podemos dizer que:
Então, podemos substituir essa expressão na equação que achamos no item (b), Passo 4:
Porém não é um dos nossos dados, então ele não pode aparecer na resposta.
Vamos utilizar a equação das forças na perpendicular à rampa sobre o bloco de massa :
Substituindo isso, temos:
Cortando , achamos que o coeficiente de atrito cinético é:
Resposta
(a)
Bloco de massa :

Bloco de massa :
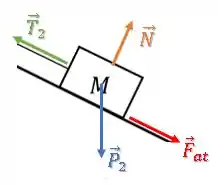
(b)
(c)