Considere que um bloco de massa desce o plano inclinado da Figura 2.
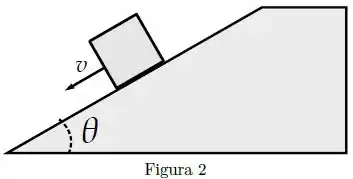
Se os coeficientes de atrito estático e cinético entre o bloco e o planos são respectivamente e , qual o módulo da força de atrito que atua sobre o bloco? Dados: , , .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Vamos dar uma olhada nas forças nesse bloquinho:
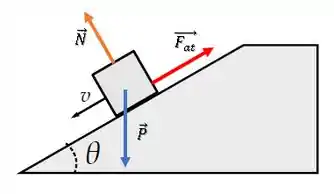
Se o nosso bloquinho está deslizando, a força de atrito é cinética.
Ou seja, a expressão da força de atrito usa o coeficiente de atrito cinético :
Passo 2
Se já temos ,,só falta achar quanto é a nossa força normal.
Para isso, vamos decompor a força peso e fazer o somatório das forças nessa direção:
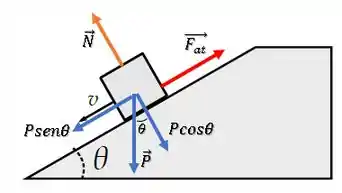
Temos um equilíbrio do bloquinho na direção perpendicular à rampa, então:
A força peso é dada por:
Logo:
Passo 3
Agora, conseguimos achar o valor da força de atrito:
Então, achamos que o módulo da força de atrito que atua sobre o bloco é . Ficamos com a letra (f).
Resposta
Letra (f)