![]()
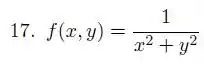
Passo 1
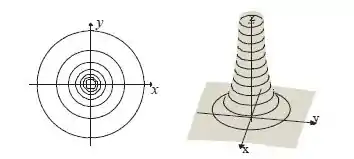
Vamos começar pelas curvas de nível.
Sempre que falamos sobre curva de nível, o que temos que fazer é igualar nossa função a uma constante qualquer.
Assim, as curvas de nível da nossa função são
E isso são várias circunferências no plano .
Tá, mas por que várias?
Porque o nosso pode assumir qualquer valor que quisermos. Assim, conforme formos mudando o valor de vamos ter circunferências diferentes, mas sempre paralelas umas as outras, porque só estaremos deslocando a circunferência.
Nossas circunferências estão centradas na origem, mas a gente tem que ficar ligado numa coisa: o raio delas é , o que significa que quanto maior for o valor de , menor será o raio da circunferência.
Temos isso aqui:
Passo 2
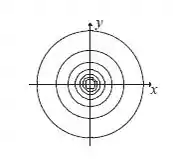
Beleza, agora que já temos as curvas de nível, precisamos identificar o gráfico da nossa função. E vamos fazer isso a partir das próprias curvas de nível.
Pensa comigo, nosso gráfico tem que ser uma figura em 3D que quando a gente cortar com planos paralelostemos que ter circunferências.
Mas, como já sabemos, os raios das nossas circunferências vão diminuindo, a medida que os nossos planos vão tendo valores de maiores.
Então, nosso gráfico tem que ter essa cara assim
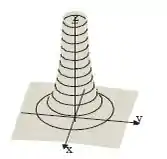
Resposta