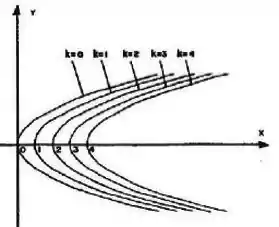
Na figura estão representadas curvas de nível da função . Escreva uma expressão adequada para .
Passo 1
Geralmente temos uma função e pedem as curvas de nível, aqui vamos ter que fazer o contrário! De cara pode parecer difícil, mas já já você vai ver que não tem mistério.
Olhando a figura, vemos que as curvas de nível da função são parábolas, voltadas pro sentido positivo do eixo .
Inclusive podemos ver que elas têm a mesma inclinação, o que muda é apenas o vértice delas, que vai se deslocando pelo eixo .
Passo 2
Repare que o vértice da curva de nível 0 é o ponto , o da curva de nível 1 é o ponto , o da curva de nível 2 o ponto e assim por diante...
Ou seja, a partir dessas observações concluímos que a curva de nível dessa função é uma parábola voltada pro sentido positivo do eixo e com vértice em .
Então essas curvas de nível são da forma
onde seria uma constante qualquer.
Passo 3
Pra achar a curvas de nível da função, temos que igualá-la a :
E ali em cima achamos
Então vamos aproveitar isso! Obtemos um sisteminha bobo:
Passo 4
Show, estamos quase lá!
Somando dos 2 lados na 1ª equação:
Agora substituindo a 2ª equação nessa:
Pronto, aí está nossa função ! :)
Viu que foi tranquilo?