Considere a função
a) Encontre o domínio e a imagem de .
b) O gráfico de é uma superfície quádrica? Se a resposta for sim, identifique a superfície e esboce o gráfico de .
c) Identifique as curvas de nível da função e esboce um mapa de contorno. Explique a relação entre o mapa de contorno e o gráfico de
Passo 1
a) Pensar em domínio de uma função é olhar para expressão dela e ver se tem denominador, raiz par ou log. Se tiver, a gente usa essas restrições aqui para criar inequações que descrevem nosso domínio:
E como a gente tem uma função de duas variáveis, nosso domínio deve ser uma região no plano , tá? Vamos lá!
Vemos que nossa função tem uma raiz par, esse argumento não pode ser negativo
Aí só temos essa restrição, então nosso domínio é dado só por essa equação mesmo. Aí escrevendo daquela forma fofa
Essa é a região onde nossa função está definida.
Passo 2
A imagem é o intervalo de valores de que nossa função assume.
Para determinar isso, gente vai fazer algo parecido ao passo anterior. Vamos olhar nossa função para ver se tem essas características:
A gente vê que a nossa função tem uma raiz par. Aí a gente pode escrever:
Aí vamos fazer aparecer a nossa função aí nessa inequação. A gente pode somar 1 dos dois lados
Prontinho, apareceu a expressão da nossa função ali na esquerda. Aí a gente diz que
Aí nossa função assume os valores no intervalo
Passo 3
b) Para a gente testar se o gráfico é uma quádrica, precisamos igualar a e dá aquela rearrumada
Ela parece um elipsoide, mas com um termo negativo, né? O que isso nos diz? Diz que ela é sim uma quádrica, o hiperboloide de uma folha (um porque só tem um termo negativo).
Passo 4
Vamos esboçar esse cara. Primeira coisa é lembrar da imagem
Então nossa função só existe acima de .
Essa superfície é aquela que tem cara de tronco de árvore. Como o termo em é o negativo, o eixo do nosso tronco vai ser paralelo ao eixo .
Comparando com a equação geral do hiperboloide de uma folha para esse caso
Essa superfície está centrada em . Ah e aquele do lado do , mostra que a interseção entre a superfície e o plano vai ser parte de uma elipse
E a interseção com o plano é uma hipérbole
Aí esboçando a parte desse tronco que só está em , nosso esboço é
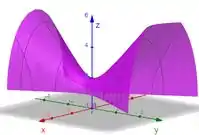
Passo 5
c) Para achar as curvas de nível, a gente precisa igualar nossa função , a valores constantes que a gente chama de .
E analisar que curvas essas expressões formam.
Mas como , temos também que
Aí nossa função é
As curvas de nível ficam
Passo 6
Agora a gente analisa essa expressão para alguns intervalos de . Uma dica é ver onde esse lado esquerdo (onde só temos as constantes) vai zerar, porque aí a gente consegue marcar uns intervalos interessantes
Como , só consideramos , aí temos os intervalos
Passo 7
Vamos olhar o que acontece em
Nesse intervalo, o termo fica negativo. Podemos fazer isso vendo .
Para escrever a equação de uma curva bonitinha, o lado das constantes precisa ser positivo, então vamos multiplicar os dois lados da equação por :
E isso são as equações de hipérboles. Como está negativo, nossa curva não toca o eixo .
Agora para :
E isso é um par de retas.
Por fim, para .
Nesse caso, esse termo da esquerda já vai ser positivo, podemos testar isso fazendo por exemplo.
Então essa uma hipérbole que não toca o eixo .
Passo 8
Aí agora é variar esse e fazer várias curvas no plano . Tendo em vista que a gente precisa representar esses intervalos onde elas são diferentes
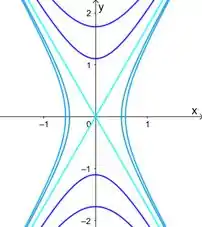
Aí a gente pode interpretar essas curvas como as projeções em das interseções entre a nossa função e os planos . É como se a gente tivesse vendo como é o nosso gráfico, visto de cima, em alturas .
Resposta
a)
b) hiperboloide de uma folha
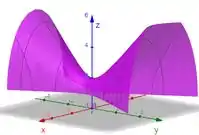
c) , hipérboles
par de retas
, hipérboles