Considere a função
a) Esboce o gráfico de .
b) Identifique a curva de nível que contém o ponto .
Passo 1
a)
Essa função é diferente porque ela é definida por partes, mas isso não afeta muito nosso procedimento pra esboçar o gráfico.
Vamos começar vendo a parte de cima, quando . Temos:
E aí, conseguiu identificar a Quádrica? E essa daqui?
Vou dar uma dica: muitos usaram o nome dessa superfície pra falar do Fred da seleção brasileira na copa do mundo de 2014 :)
É a clássica equação de um cone! Ou melhor, sendo mais rigoroso, a metade superior de um cone circular:
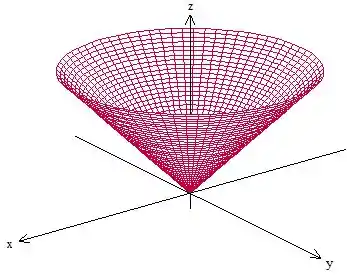
Se você reconheceu essa mas não a outra, você provavelmente caiu no dibre da questão, que foi acrescentar um , um sinal negativo, só pro aluno se perder.
Passo 2
Enfim, a superfície vai ser que nem esse cone aí da figura mas virado pra baixo e deslocado de pra cima no eixo !
Também não podemos esquecer que estamos na região . Ou seja, como
E o que tá dento da raiz tem que estar entre 0 e 16, temos
Perceba que na sua altura mínima, , vamos ter uma circunferência de raio :
Depois o cone sobe até atingir o ponto do James Bond: .
A partir disso tudo, podemos esboçar tranquilamente esse gráfico!
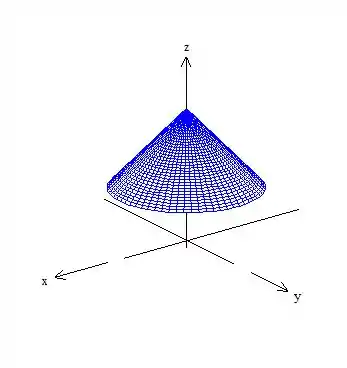
Passo 3
Mas ainda falta a outra parte da função, quando :
Vamos dar uma melhorada nisso elevando ao quadrado (mas tem que tomar cuidado, vou explicar o porquê):
Isso é a equação de uma esfera de raio 5 centrada na origem!
Eu disse que temos que tomar cuidado quando elevamos ao quadrado porque a nossa função de origem é . Então na verdade a superfície é a metade superior da esfera, show?
Passo 4
Agora, que nem fizemos pro cone, vamos ver como é limitada essa esfera.
Quando temos
Mas vimos que , então nesse caso .
Passo 5
Agora, quando temos
Passo 6
Então o gráfico dessa parte da função é um pedaço de uma semiesfera de raio centrada na origem, que vai da altura até .
Saca só o gráfico dela:
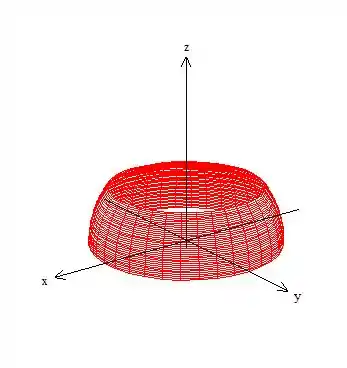
Passo 7
Mas ele pediu gráfico da função . Pra isso basta juntar os 2 gráficos que achamos, o do cone com o da esfera!
Assim o gráfico de é:
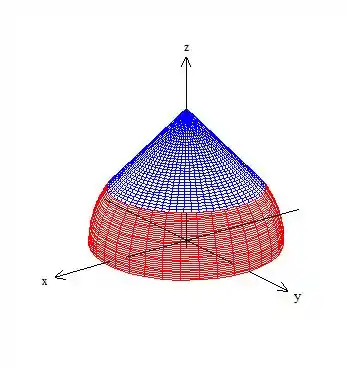
Passo 8
b)
Como essa função é definida por partes, a primeira coisa que temos que fazer é determinar em qual parte da função o ponto se encontra. E isso vai ser bem simples, basta a gente calcular pro ponto :
E como , temos que considerar a parte de cima da função, dada por
Passo 9
Assim, temos
Portanto, o ponto pertence à curva de nível da função. Vamos ver que curva é essa?
Passo 10
Igualando a equação da função a :
Ótimo! Então a curva de nível que contém o ponto é uma circunferência de raio centrada no ponto .
Resposta
a)
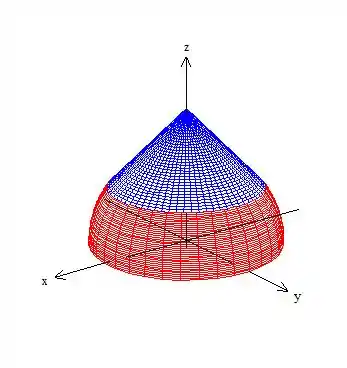
b)
Uma circunferência de raio centrada no ponto .