Considere as regiões do plano
Seja
- Esboce hachurado. Esboce ao lado a fronteira de , denotada por .
- Determine as constantes e as funções tal que
- Descreva o conjunto usando igualdades e desigualdades.
Passo 1
Vamos lá galera, a questão aqui pede pra gente esboçar essa região, que na verdade é a interseção de duas regiões, vamos fazer cada uma de uma vez! Além disso, ele quer que a gente desenhe também somente a fronteira da região. Já que a prova pede, quem somos nós pra dizer não, né? Bora lá pros esboços.
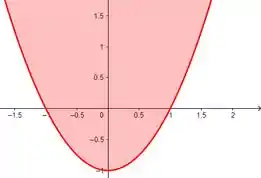
Vamos começar pela região :
Se tivéssemos um sinal de igual, isolando o , teríamos:
E isso nada mais é do que uma parábola, com a concavidade virada para cima (pois o coeficiente do é positivo) e que corta o eixo em . Acontece que como temos o sinal de não estamos falando somente da parábola, mas sim de tudo que é maior ou igual a essa parábola. Ou seja, nossa região é isso daqui:
Passo 2
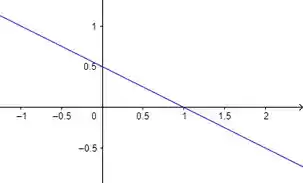
Vamos fazer o mesmo processo pra região .
Colocando sinal de igual e isolando o :
E teríamos uma reta. Mas como temos aquele sinal de menor ou igual, na real o que temos é tudo o que está abaixo da reta, assim:
Passo 3
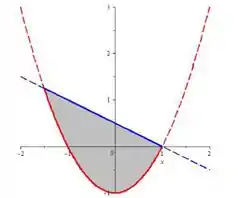
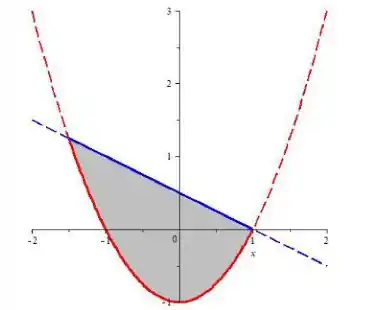
Agora, juntando as duas coisas, teremos a região , assim:
E agora, para esboçar a fronteira, é só a gente tirar esse hachurado de dentro (porque a gente só quer o que está em volta) e tirar esse tracejado que não faz parte da nossa região, assim:
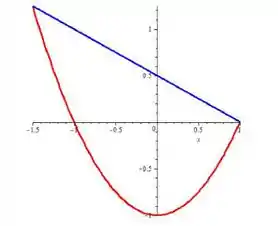
Passo 4
Agora aqui na letra a questão pede pra gente formalizar as coisas e definir matematicamente a nossa região .
.
.
.
Pra que né?! Já não bastava ter que desenhar essa bagaça.............
Mas vamos lá né, fazer o que
.
.
.
Matematicamente, temos que ter
O desenho, para nos ajudar, é
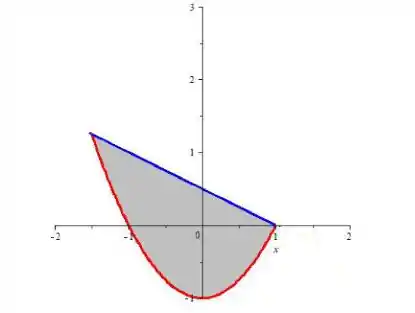
Mas na real, se a gente parar pra pensar, eu reclamei só porque sou rabugenta, porque essa parte nem vai ser tão difícil assim. Olha só:
A gente definiu essa curva vermelha a partir da região e chegamos na equação da parábola:
E definimos a curva azul (que na verdade é uma reta), a partir da região e chegamos em
Assim, as funções que definem a nossa região são essas duas aí que a gente JÁ achou. Só precisamos dar nome aos bois.
Podemos dizer que
Assim,
Mas e o e o , quem são?
Ora, mais fácil ainda, só olhar na figura!
Nossa região tá indo de até
Mas se você não acredita muito na figura, pode fazer também
Que você vai encontrar esses valores para , tá bem?
Pra fechar a conta e passar a régua então, a definição matemática da nossa região ficou
Passo 5
Aqui na letra a gente precisa dizer a parte da fronteira do nosso conjunto que está abaixo do eixo , ou seja, onde .
Se olharmos nosso esboço
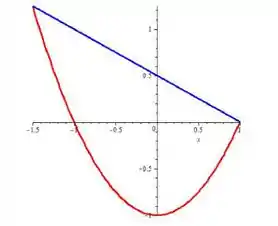
Vemos que abaixo do eixo a fronteira é formada somente pela parábola.
Portanto, a interseção da fronteira de com é dada pela parte da parábola com o variando entre e . Matematicamente, usando igualdades e desigualdades, como a questão pede:
Resposta