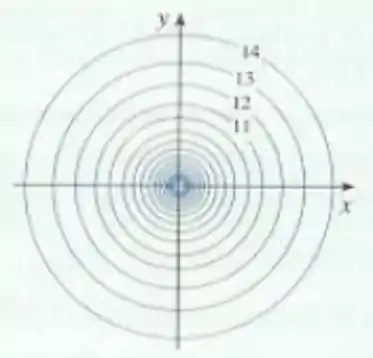
Um mapa de contorno de uma função é mostrado. Use-o para fazer um esboço do gráfico da .
Passo 1
Vamos observar o mapa de contorno com calma.
Primeiramente, podemos ver que as curvas de nível dessa função são circunferências centradas na origem. Outra coisa, ele indicou os níveis de algumas curvas: podemos ver que o raio das circunferências vai aumentando conforme o nível das curvas vai subindo.
Agora ficou fácil! Pra esboçar esse gráfico basta a gente ter em mente que as curvas de nível são fatias do gráfico.
Ou seja, se passarmos uma faca horizontalmente (visualiza mesmo que ajuda!) no gráfico dessa função numa altura , vamos obter uma circunferência, com centro em , e quanto maior for , maior será seu raio!
Passo 2
Aqui é importante a gente reparar que as circunferências vão aumentando cada vez mais devagar. Isto é, no começo elas estão bem próximas, mostrando que o gráfico cresce rápido, e depois elas estão mais espaçadas, o que mostra uma desaceleração no crescimento do gráfico.
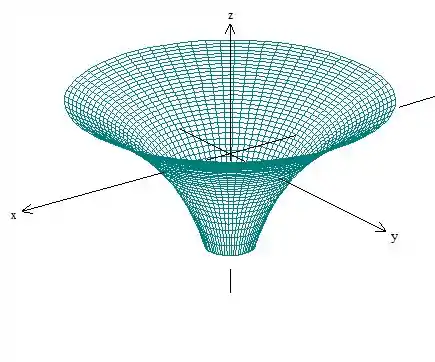
Enfim, o gráfico é meio genérico, mas ele deveria ficar mais ou menos assim:
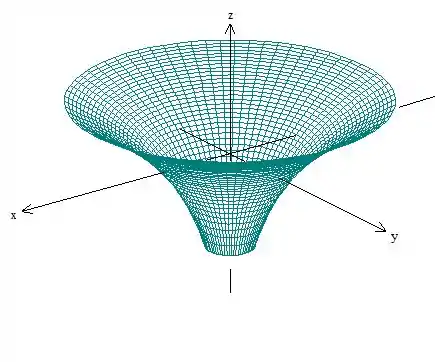
Resposta