UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 14
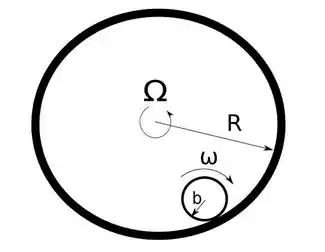
Uma bola de raio e massa está rolando sem deslizar sobre um anel de raio . A velocidade angular da bola é . Suponha que o anel está rodando com uma velocidade angular . Qual é a velocidade linear do centro de massa da bola em relação ao centro do anel? Escreva sua resposta com as variáveis do exercício.
Passo 1
Oii pessoal, tudo bem com vocês?
Nessa questão temos aqueles problemas tipo das bonecas russas sabe? Uma bola girando dentro de um anel que tá girando de uma roda que tá girando dentro de... brincadeira galera.
O que temos é uma bola girando dentro de um anel que também está girando. Essa bola possui raio e gira com velocidade angular , enquanto o anel gira com velocidade angular e possui raio .
Precisamos determinar a velocidade linear do centro de massa da bola em relação ao centro do anel.
A ideia principal aqui é separarmos os movimentos galera! É o famoso princípio da superposição.
Vamos primeiro analisar o efeito no centro de massa da bola estar rotacionando com velocidade angular . Depois, analisamos o efeito da bola estar apoiada sob o anel que rotaciona com .
Por fim, superpomos os dois efeitos. Beleza?
Então, vamo nessa!
Passo 2
Vamos começar pensando na rotação da bola em torno do seu próprio centro. A bola roda sem deslizar na superfície interna com velocidade angular Como ela roda sem deslizar o seu ponto de contato com a superfície do anel está sempre com velocidade nula, por isso podemos afirmar que ele é um centro instantâneo de rotação (C.I.R).
Daí, pra descobrirmos a velocidade linear do centro de massa da bolinha, podemos usar que dado um C.I.R e um ponto qualquer do corpo que gira:
Onde é a distância entre o C.I.R e o ponto, e é a velocidade linear desse ponto.
No caso da nossa bola, podemos dizer que:
Excelente! O centro de massa fica rotacionando em torno do centro do anel com uma velocidade linear (devido somente ao movimento de rotação da bola) que vale:
Essa velocidade é tangente à trajetória do centro de massa da bola em cada instante, ou seja, é tangente a uma circunferência de raio:
Tranquilo até aqui? Vamos prosseguir 😊
Passo 3
Bom, vamos pensar agora no movimento de rotação do anel.
Como a bola está apoiada no anel, e o anel rotaciona com velocidade angular , a bola também está rotacionando com em torno do centro do anel.
E, mais importante ainda, o seu centro de massa também rotaciona com em torno do anel. Por causa dessa rotação, podemos dizer que é imprimida ao CM da bola uma velocidade linear que vale:
(Pois, como comentamos, é o raio da trajetória do CM da bola).
Passo 4
Perfeito pessoal, chegou a hora de superpor as coisas!!
O CM da bola tem uma velocidade linear devida à rotaç��o da bola e outra devido à rotação do anel. Assim, podemos afirmar que:
Onde:
Além disso, ambos vetores apontam sempre na direção tangencial à trajetória do CM (uma circunferência de raio em torno do cento do anel). E, não apenas a mesma direção, mas também o mesmo sentido, já que tanto o anel como a bola giram no mesmo sentido.
Logo:
Prontinho pessoal! Curtiram a solução? Responde Aí!