A corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
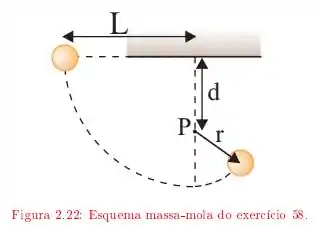
Mostre que para que a bola faça uma volta completa em torno do pino (Sugestão: A bola ainda deve estar se movendo quando chegar ao ponto mais alto da trajetória).
Passo 1
Olá gente, como vocês estão?
Nessa questão temos uma bolinha que está presa a um fio de comprimento . Ela é largada da posição horizontal, conforme mostrado na figura, e realiza uma trajetória circular até que o seu fio encontra o ponto .
Nesse momento a bola começa a girar em torno desse ponto .
Nesse item precisamos provar que, se a bola completar uma volta completa em torno do ponto é válido que:
Para fazer isso, precisamos pensar sobre qual é a condição para a bola conseguir realizar uma volta completa em torno do ponto .

Para que ela não “caia” durante a volta a corda precisa estar sempre tracionada, ou seja, . E, o ponto mais crítico para a tração na corda acontece justamente no ponto mais alto da trajetória após a corda tocar o pino.
Ainda tá complicado? Não se preocupa, vamos com bastante calma resolver todos os detalhes dessa questão 😉
Passo 2
Bom, como calculamos no item anterior, utilizando a conservação da energia mecânica, vimos que a bola chega ao ponto mais alto da trajetória ao redor do pino com velocidade:
Até aí beleza...
No ponto mais alto da trajetória, como trata-se de uma trajetória circular, teremos uma força centrípeta, que nada mais é do que a resultante radial das forças na partícula. Assim:
Daí, substituindo, temos:
Como na direção radial, no ponto mais alto da trajetória, atuam apenas o peso da bola e a tração, vem que:
Massa!
Como falamos anteriormente, para que a bola seja capaz de completar o loop ao redor do pino, a tração não pode ser nula em nenhum momento. Ou seja:
Assim, temos:
Logo:
Como:
Temos:
Portanto, chegamos que:
Essa é a condição que precisa ser obedecida para a bola conseguir realizar o movimento de loop. Como queríamos provar 😊
Prontinho gente, obrigado pela atenção de todos!!
Resposta
Resposta no texto.