Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 411234567891011121314151617181920212223242526272829303132333435363738394042434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

13) Seja S a superfície do sólido limitado inferiormente pelo paraboloide z = x 2 + y 2 e superiormente pelo plano z = 1 . Se a densidade de massa é dada por ρ x ,   y ,   z = z , calcule a massa de S .

Passo 1

Bem, uma massa de uma superfície S é nos dado agora por uma integral de superfície escalar e sua cara é...

M S = ∬ S   ρ x ,   y ,   z   d S

No caso, ρ x ,   y ,   z é a função de densidade que já já descobriremos quem é. ;)

Bem, como estamos trabalhando com uma integral de superfície, podemos muito bem utilizar o passo a passo maroto para detonar o problema imposto:

  1. 1º - Parametrizar a superfície S .
  2. 2º - Substituir os termos da parametrização na função ρ ( x ,   y ,   z ) .
  3. 3º - Encontrar o termo d S .

Passo 2

Vamos resolver então o primeiro passo de resolução de integral de superfície parametrizando S . Por falar nisso, quem é a superfície?

Para termos uma noção do que fazermos, recomendo fortemente que a desenhe. E pelo enunciado, ele é a superfície que delimita o sólido entre o paraboloide e o plano z = 1 :

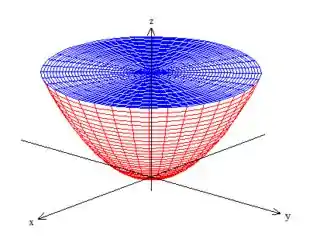
Então a superfície S , por ser a “envoltório” do sólido, é a junção do pedacinho de plano que vamos chamar de S 1 e do paraboloide que vamos chamar de S 2 . Ou, em matemática dizemos que...

S = S 1 ∪ S 2

Se queremos a massa de S , então façamos...

M S = ∬ S   ρ x ,   y ,   z   d S =

∬ S 1   ρ x ,   y ,   z   d S + ∬ S 2   ρ x ,   y ,   z   d S

Percebeu? Então teremos que editar duas integrais de superfícies, e para cada uma seguir o passo a passo. Bora?

Passo 3

Vamos começar com a primeira integral de superfície:

∬ S 1   ρ x ,   y ,   z   d S

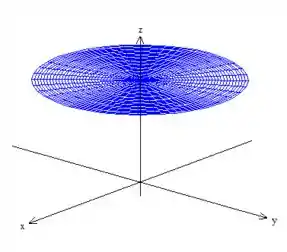
Onde devemos parametrizar S 1 como primeira tarefa. Como S 1 é um plano z = 1 , façamos uma parametrização explícita...

x = x

y = y

z = 1

Onde x e y continuam os mesmos pelo fato de eles serem os parâmetros...

r → x ,   y = x ,   y ,   1

No caso, como podemos ver olhando para a projeção de S 1 sobre o plano x y (onde os parâmetros variam), vemos...

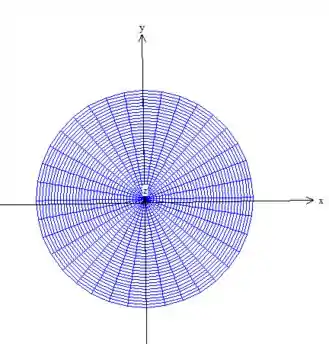
Um círculo, que é o resultado da intersecção do plano z = 1 com o paraboloide z = x 2 + y 2 ...

z = x 2 + y 2       →           1 = x 2 + y 2

Ou seja, um círculo de raio 1 , mas por hora apenas digamos que x e y variam no círculo D (apenas para que não percamos o foco na integral de superfície):

x   e   y ∈ D

Passo 4

Substituindo a função que estamos integrando

ρ x ,   y ,   z = z

Pelos termos da parametrização...

r → x ,   y = x ,   y ,   1

Só teremos que mudar o z ...

ρ r → x ,   y = 1

Passo 5

Beleza! Então podemos sair em busca do termo d S ...

d S = N →   d x d y

Onde esse vetor normal é dado por...

N → = ∂ r → x ,   y ∂ x × ∂ r → x ,   y ∂ y

Porém, como estamos trabalhando com uma parametrização em forma de um gráfico de função...

z = f x ,   y = 1

Podemos utilizar o bizu de vetor normal para esse caso:

N → = - ∂ f ∂ x ,   - ∂ f ∂ y ,   1

N → = 0 ,   0 ,   1

Bem, ainda não concluímos o termo d S , pois ele nos exige o módulo de N → , então devemos extrair a raiz quadrada...

N → = 0 2 + 0 2 + 1 2

N → = 1

d S = 1   d x d y

Passo 6

Voltando para integral de linha que estamos resolvendo em S 1 ...

∬ S 1   ρ x ,   y ,   z   d S

E substituindo esses termos que determinamos (lembrando que S 1 , trocamos por D que é a região de variação de x e y ).

∬ S 1   ρ x ,   y ,   z   d S = ∬ D   1 ⋅     1 d x d y =

  ∬ D     d x d y

Integral de 1 d x d y em D é a área de D e como ele é um círculo de raio 1 ( x 2 + y 2 = 1 )...

∬ D     d x d y = π 1 2 = π

Passo 7

Agora repetiremos o processo para a segunda integral de superfície que estamos resolvendo...

∬ S 2   ρ x ,   y ,   z   d S

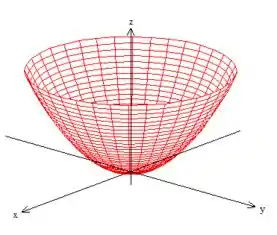
Como S 2 é o paraboloide z = x 2 + y 2 ...

Podemos parametriza-lo também como um a parametrização explícita, ondo os parâmetros novamente são x e y ...

x = x

y = y

z = x 2 + y 2

Então...

r → x ,   y = x ,   y ,   x 2 + y 2

Onde novamente x e y pertencem a projeção no plano x y que é o mesmo círculo de raio 1 :

x ,   y ∈ D

Passo 8

Substituindo a função que estamos integrando

ρ x ,   y ,   z = z

Pelos termos da parametrização...

r → x ,   y = x ,   y ,   x 2 + y 2

Só teremos que mudar o z ...

ρ r → x ,   y = x 2 + y 2

Passo 9

Novamente, encontrando o valor de d S pelo bizu de parametrização como gráfico de função explícita...

z = f x ,   y = x 2 + y 2

N → = - ∂ f ∂ x ,   - ∂ f ∂ y ,   1

N → = - 2 x ,   - 2 y ,   1

d S = N → d x d y

d S = - 2 x 2 + - 2 y 2 + 1 2   d x d y

d S = 4 x 2 + 4 y 2 + 1   d x d y   →

d S = 4 x 2 + y 2 + 1   d x d y

Passo 10

Voltando para a integral de superfície, mas dessa vez com a superfície S 2 ...

∬ S 2   ρ x ,   y ,   z   d S

E substituindo tudo...

∬ D   x 2 + y 2 4 x 2 + y 2 + 1   d x d y

Como D é uma região circular, pelas coordenadas polares...

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

x 2 + y 2 = r 2

Como o r e o θ variando de...

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Substituindo:

∬ D   x 2 + y 2 4 x 2 + y 2 + 1   d x d y = ∫ 0 2 π ∫ 0 1 r 2 4 r 2 + 1 ⋅ J   d r d θ =

∫ 0 2 π ∫ 0 1 r 2 4 r 2 + 1 ⋅ r   d r d θ

Calculando a integral de dentro em r fazendo uma mudança:

∫ 0 2 π ∫ 0 1 r 2 4 r 2 + 1 ⋅ r   d r d θ =

4 r 2 + 1 = t       →           d t = 8 r d r           →             r d r = d t 8

Trocando os limites também...

r = 0         →             t = 4 0 2 + 1 = 1

r = 1         →             t = 4 1 2 + 1 = 5

Esse r 2 sozinho também deve estar em termos de t ...

4 r 2 + 1 = t         →           r 2 = t - 1 4 = t 4 - 1 4

Trocando tudo...

∫ 0 2 π ∫ 0 1 r 2 4 r 2 + 1 ⋅ r   d r d θ = ∫ 0 2 π ∫ 1 5 t 4 - 1 4 t d t 8 d θ =

1 8 ∫ 0 2 π ∫ 1 5 t 3 2 4 - t 1 2 4 d t d θ =

1 8 ∫ 0 2 π 2 5 t 5 2 4 - 2 3 t 3 2 4 1 5 d θ = 1 8 ∫ 0 2 π t 2 t 10 - t t 6 1 5 d θ =

1 8 5 2 5 10 - 5 5 6 - 1 10 - 1 6 ∫ 0 2 π d θ =

1 8 25 5 - 1 10 - 5 5 - 1 6 2 π =

1 8 3 ⋅ 25 5 - 3 - 25 5 + 5 30 2 π =

1 4 50 5 + 2 30 π = 1 4 25 5 + 1 15 π =

25 5 + 1 60 π

Passo 11

Lembrando que o que queremos é a massa de S ...

M S = ∬ S 1   ρ x ,   y ,   z   d S + ∬ S 2   ρ x ,   y ,   z   d S

Somando os dados obtidos paralelamente...

M S = 25 5 π + π 60 + π =

M S = 25 5 π + 61 π 60 =

π 60 25 5 + 61

Resposta

π 60 25 5 + 61

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1