Calcule as seguintes integrais de superfícies:

onde é a parte do plano limitada pelo cilindro

Bom, no enunciado nos foi dada:

Assim, temos que:

Além disso, a superfície dada trata-se do plano:

Na parte que é limitado pelo cilindro .

Vamos seguir nossa receitinha de bolo!

Parametrizar a superfície :

A superfície é a parte do plano que está dentro do cilindro .

Para entender melhor, vamos esboçar essa região:

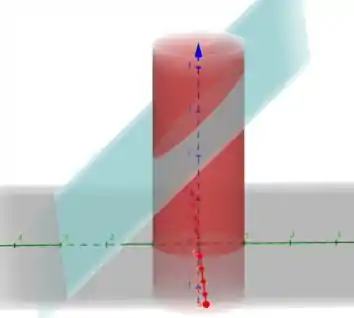
A nossa região de interesse é uma elipse dentro do plano. Para parametrizar essa superfície, vamos usar a parametrização elíptica:

onde e .

Além disso, pela relação de , temos:

Perfeito então! Temos a parametrização:

Massa! Vamos para a próxima etapa.

Escrever a função como função da parametrização:

Vimos que a nossa função vale:

Mas, pela parametrização:

Logo:

Calcular o módulo do vetor normal à superfície, usando que:

Vamos lá, encontramos que:

Assim:

Já se tomarmos a derivada parcial com relação a , teremos:

Muito bom! Vamos então calcular o produto vetorial:

Daí, tirando o módulo temos:

Montar a integral:

Com as informações que descobrimos nas etapas anteriores, temos que:

Excelente! Nossa missão agora se resume a resolver essa integral dupla.

Vamos resolver a integral:

Colocando as constantes pra fora:

Usando que:

Temos:

Resolvendo a integral interna, ficamos com:

Logo:

Portanto, finalmente concluímos que:

Excelente galera! Até a próxima 😊