Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar

Ver Teoria
Exercício 341234567891011121314151617181920212223242526272829303132333536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

4) Calcule a área das superfícies:

e) S : superfície gerada pela rotação do conjunto C = 0 , y ,   z ∈ R 3 ; y - 2 2 + z 2 = 1 em torno do eixo z .

Passo 1

Então, área de superfície para nós a parir deste momento será dado por uma integral de superfície escalar bem especial. Essa daqui, oh:

A S = ∬ S   1   d S

Como toda e boa integral de superfície escalar vamos seguir um passo a passo maroto que nos ajudará muito:

1º - Parametrizar a superfície S .

2º - Encontrar o termo d S .

Passo 2

Precisamos da superfície parametrizada, as antes, quem é mais vantajoso nos perguntarmos quem é a superfície S ?

Bem, como o próprio problema nos indicou, a superfície é obtida girando a circunferência no plano z y , y - 2 2 + z 2 = 1 (ela está no plano z y , pois a coordenada x é 0 , 0 , y ,   z ∈ R 3 ):

Repare que é uma circunferência de raio 1 deslocada de 2 unidades em y . Quando girarmos ao redor do eixo z ...

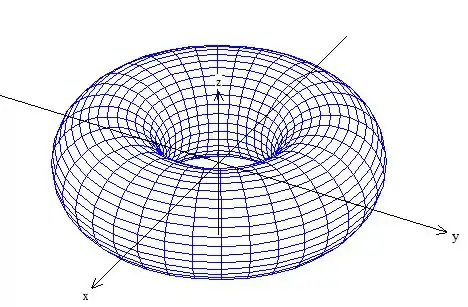
Eis a superfície !

Passo 3

Uma superfície como essa, foi gerada com uma revolução, logo a parametrização que devemos utilizar é a parametrização que chamamos de parametrização de superfícies de revolução. Bem sugestivo, neh? kkkkkk

Para essa superfície, como você já sabe, primeiro parametrizamos a curva que deu origem, no caso, a circunferência deslocada:

y - 2 2 + z 2 = 1

Podemos parametriza-la de forma parecida com as coordenadas polares se atentando que ela está deslocada em y e, além disso, o raio dela é 1 ...

z = 1 sin ⁡ t

y = 2 + 1 cos ⁡ t

Logo a parametrização da curva é...

r → t ,     ? =   ?     ,   2 + sin ⁡ t , cos ⁡ t

Repare que ficaram uns vácuos ali! Isso porque a uma curva precisa de uma única variável e a superfície de duas, bora encontrar a segunda?

Passo 4

Bem, o segundo parâmetro é o ângulo θ que chamamos de fator de giro. Como no caso estamos girando ao redor de z ou seja, no plano x y ...

Devemos colocar uma correção com um cosseno e um seno em x e y . O cosseno, se quisermos o ângulo saindo do eixo x no sentido anti-horário como no desenho acima, deve ser necessariamente o x e o y o seno:

x = cos ⁡ θ

y = sin ⁡ θ

Então a parametrização fica...

r → t ,     ? =   ?     ,   2 + cos ⁡ t , sin ⁡ t             →                 r → t ,   θ = cos ⁡ θ ,   2 + cos ⁡ t sin ⁡ θ ,   sin ⁡ t           →

Como tem um cara com t na frente do seno de θ , tem que ter na frente do cosseno também:

r → t ,   θ = 2 + cos ⁡ t cos ⁡ θ ,   2 + cos ⁡ t sin ⁡ θ ,   sin ⁡ t

Eis a parametrização!

Passo 5

Ok, agora nos falta a segunda parte do problema que é encontrar o domínio dos parâmetros: onde eles estão variando.

Bem, se olharmos para a superfície de cima pra baixo z para obter a variação de θ (pois é ele quem varia no x e y )...

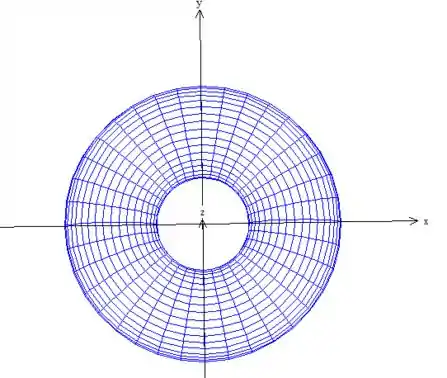
Como pode ver na projeção da superfície no plano x y , precisamos de um θ dando uma volta completa:

0 ≤ θ ≤ 2 π

Enquanto isso, o t representa o ângulo de giro no plano z y , pois foi nesse plano que tiramos a parametrização da curva:

Como temos uma volta completa também...

0 ≤ t ≤ 2 π

Passo 6

Beleza, então com essa primeira etapa já resolvida podemos sair em busca do termo d S ...

d S = N →   d t d θ

Onde esse vetor normal é dado por...

N → = ∂ r → t ,   θ ∂ t × ∂ r → t ,   θ ∂ θ

Não precisa se preocupar com a ordem dessas derivadas parciais, pois o módulo no d S corrige qualquer sinal de menos ( ). Por falar nisso, calculando essas derivadas parciais...

r → t ,   θ = 2 + cos ⁡ t cos ⁡ θ ,   2 + cos ⁡ t sin ⁡ θ ,   sin ⁡ t             →

  ∂ r → t ,   θ ∂ t = - sin ⁡ t cos ⁡ θ , - sin ⁡ t sin ⁡ θ , cos ⁡ t

∂ r → t ,   θ ∂ θ = - 2 + cos ⁡ t sin ⁡ θ ,   2 + cos ⁡ t cos ⁡ θ ,   0

Substituindo tudo dentro do produto vetorial (um determinante lembrando em que a primeira linha estão os vetores i → , j → e k → ...

N → = ∂ r → t ,   θ ∂ t × ∂ r → t ,   θ ∂ θ

N → = i → j → k → - sin ⁡ t cos ⁡ θ - sin ⁡ t sin ⁡ θ cos ⁡ t - 2 + cos ⁡ t sin ⁡ θ 2 + cos ⁡ t cos ⁡ θ 0                 →

N → = - 2 cos ⁡ t sin ⁡ θ - cos 2 ⁡ t sin ⁡ θ j → + - 2 sin ⁡ t cos 2 ⁡ θ - sin ⁡ t cos ⁡ t cos 2 ⁡ θ k → - 2 cos ⁡ t cos ⁡ θ + cos 2 ⁡ t cos ⁡ θ i → + 2 sin ⁡ t sin 2 ⁡ θ + sin ⁡ t cos ⁡ t sin 2 ⁡ θ k → =

N → = - 2 cos ⁡ t cos ⁡ θ - cos 2 ⁡ t cos ⁡ θ i → + - 2 cos ⁡ t sin ⁡ θ - cos 2 ⁡ t sin ⁡ θ j → + - 2 sin ⁡ t cos 2 ⁡ θ + sin 2 ⁡ θ - sin ⁡ t cos ⁡ t cos 2 ⁡ θ + sin 2 ⁡ θ k → =

N → = - 2 cos ⁡ t cos ⁡ θ - cos 2 ⁡ t cos ⁡ θ i → + - 2 cos ⁡ t sin ⁡ θ - cos 2 ⁡ t sin ⁡ θ j → + - 2 sin ��� t - sin ⁡ t cos ⁡ t k → =

N → = cos ⁡ t cos ⁡ θ - 2 - cos ⁡ t i → + cos ⁡ t sin ⁡ θ - 2 - cos ⁡ t j → + sin ⁡ t - 2 - cos ⁡ t k →

Então

N → = cos ⁡ t cos ⁡ θ - 2 - cos ⁡ t , cos ⁡ t sin ⁡ θ - 2 - cos ⁡ t ,   sin ⁡ t - 2 - cos ⁡ t

Bem, ainda não concluímos o termo d S , pois ele nos exige o módulo de N → , então devemos extrair a raiz quadrada...

N → = cos ⁡ t cos ⁡ θ - 2 - cos ⁡ t 2 + cos ⁡ t sin ⁡ θ - 2 - cos ⁡ t 2 + sin ⁡ t - 2 - cos ⁡ t 2

N → = - 2 - cos ⁡ t 2 cos 2 ⁡ t cos 2 ⁡ θ + cos 2 ⁡ t sin 2 ⁡ θ - 2 - cos ⁡ t 2 + sin 2 ⁡ t - 2 - cos ⁡ t 2

N → = - 1 2 + cos ⁡ t 2 cos 2 ⁡ t cos 2 ⁡ θ + sin 2 ⁡ θ + sin 2 ⁡ t

N → = - 1 2 2 + cos ⁡ t 2 cos 2 ⁡ t + sin 2 ⁡ t

N → = 2 + cos ⁡ t 2

N → = 2 + cos ⁡ t

Como o cosseno, no mínimo é - 1 , o interior desse módulo continua positivo, logo...

d S = 2 + cos ⁡ t   d t d θ

Passo 7

Voltando para integral de linha que estamos resolvendo...

∬ S   1   d S

E substituindo esses termos que determinamos (lembrando que S , trocamos por D que é a região de variação de z e θ ).

A s = ∬ S   1   d S = ∬ D     2 + cos ⁡ t   d t d θ

Lembrando que D foi dividido em duas partes, a primeira é:

0 ≤ θ ≤ 2 π

0 ≤ t ≤ 2 π

Gerando a integral

∫ 0 2 π ∫ 0 2 π 2 + cos ⁡ t   d t d θ =

∫ 0 2 π ∫ 0 2 π 2 + cos ⁡ t   d t d θ =

∫ 0 2 π 2 t + sin ⁡ t 0 2 π d θ =

∫ 0 2 π 4 π d θ =

4 π 2 π =

8 π 2

Resposta

8 π 2

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z = c
Calcule a integral de superfície. ∬ x 2 y z d S S é a parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × 0,2 .
Determine a área da superfície.A parte do cone z = x 2 + y 2 que se encontra entre o plano y = x e o cilindro y = x 2 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de um a integral unidimensional e usando sua calculadora para estimar a integral.A Parte da superfície z =
Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1