4) Calcule a área das superfícies:
a) porção do plano , que está dentro do cilindro .
Passo 1
Então, área de superfície para nós a parir deste momento será dado por uma integral de superfície escalar bem especial. Essa daqui, oh:
Como toda e boa integral de superfície escalar vamos seguir um passo a passo maroto que nos ajudará muito:
1º - Parametrizar a superfície .
2º - Encontrar o termo .
Passo 2
Precisamos da superfície parametrizada, mas antes, é mais vantajoso nos perguntarmos quem é a superfície ?
Bem, como o próprio problema nos indicou, é um pedaço do plano azul

Dentro do cilindro:
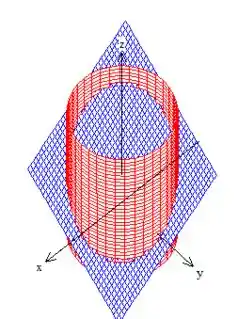
Não se preocupe na hora de fazer um esboço, afinal isso é apenas para nos dar uma noção de quem que estamos trabalhando. O que queremos mesmo é parametrizar isso daí, então bora?
Passo 3
Bem, estamos lidando com um plano com uma equação bem legal onde podemos definir de forma explícita em termos de e ...
Se levarmos em consideração que uma superfície têm dois parâmetros, a nossa já está parametrizada em termos de e ...
Passo 4
Ok, agora nos falta a segunda parte do problema que é encontrar o domínio dos parâmetros: onde eles estão variando.
Bem, a superfície é um plano, mas ela está sendo delimitado dentro de um cilindro...
Se olharmos para a projeção dessa superfície no plano , o que vamos ver é exatamente esse disco de raio igual ao do cilindro delimitador... :
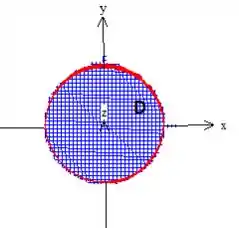
No momento, digamos apenas que e variam dentro de .
Passo 5
Beleza, então com essa primeira etapa já resolvida podemos sair em busca do termo ...
Onde esse vetor normal é dado por...
Não precisa se preocupar com a ordem dessas derivadas parciais, pois o módulo no corrige qualquer sinal de menos ( ). Por falar nisso, calculando essas derivadas parciais...
Substituindo tudo dentro do produto vetorial (um determinante lembrando que a primeira linha são os vetores , e ...
Então
Bem, ainda não concluímos o termo , pois ele nos exige o módulo de , então devemos extrair a raiz quadrada...
Passo 6
Voltando para integral de linha que estamos resolvendo...
E substituindo esses termos que determinamos (lembrando que , trocamos por que é a região de variação de e ).
Epa! Essa integral dupla aí é a área da região e como a ela é uma circunferência...
O raio dela é ...