Monte, mas não calcule, uma integral iterada à integral de superfície dada projetando no
- Plano
- Plano
- Plano
Onde é a porção do plano no primeiro octante.
Passo 1
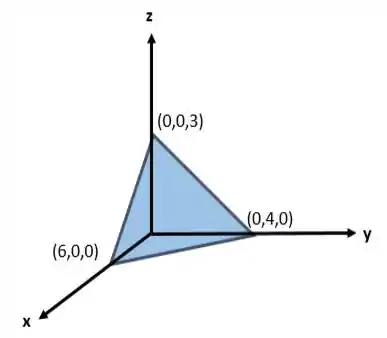
a) Calma, é muita informação! Vamos organizar as informações e ver o que ele quer na questão! Primeiro vamos entender a superfície , que é um plano no primeiro octante.
Para desenhar um plano é interessante ver a interseção dele com cada eixo e ligar os pontos:
Para e
Para e
Para z e
Assim a imagem do plano é:
Passo 2
Primeiro vamos fazer a integral projetada no plano , assim, devemos ter somente e variando. Então, devemos substituir e substituir na integral, logo:
Mas quando formos achar a integral iterada à integral de superfície dada projetada em , precisaremos multiplicar o módulo do vetor normal a superfície . Deste modo, vamos fazer a parametrização explicita.
Podemos então fazer a parametrização explícita como abaixo
Como o módulo da normal para a parametrização explícita é:
Como,
Temos que:
Agora podemos montar a integral não esquecendo de multiplicar . Assim a integral fica,
Passo 3
Vamos fazer o mesmo para as outras duas integrais. No plano vamos fazer somente e variando, assim, devemos encontrar e substituir na integral, logo:
A parametrização explícita é dada por
Como o módulo da normal para a parametrização explícita é:
Como,
Temos que:
Assim a integral fica:
Passo 4
Para a última integral. No plano vamos fazer somente e variando, assim, devemos encontrar e substituir na integral, logo:
A parametrização explícita é dada por
Como o módulo da normal para a parametrização explícita é:
Como,
Assim a integral fica:
Passo 5
O próximo passo é encontrar o limites de integração para cada integral. Ou seja, precisamos descobrir o domínio . Mas antes de começar, vamos relembrar aquelas três contas que fizemos para montar o gráfico no Passo 1:
Para e
Para e
Para z e
No plano , temos que o valor de é igual a zero. Logo, para um valor fixo de , vamos avaliar a variação de :
Como estamos tratando do primeiro octante, não pode ser negativo, variando de
Olhando para equações, podemos ver que o valor máximo que pode ter é . Ou seja,
Colocando os limites de integração na integral temos,
No plano , vamos seguir o mesmo raciocínio. Só que agora temos que o valor de é igual a zero. Logo, para um valor fixo de , vamos avaliar a variação de :
Assim,
Colocando os limites de integração na integral temos,
Por fim, no plano , temos que o valor de é igual a zero. Logo, para um valor fixo de , vamos avaliar a variação de :
Assim,
Colocando os limites de integração na integral temos,
Resposta
Assim temos que as integrais são: