4) Calcule a área das superfícies:
d) parte do cilindro , limitado pelo plano e o .
Passo 1
Então, área de superfície para nós a parir deste momento será dado por uma integral de superfície escalar bem especial. Essa daqui, oh:
Como toda e boa integral de superfície escalar vamos seguir um passo a passo maroto que nos ajudará muito:
1º - Parametrizar a superfície .
2º - Encontrar o termo .
Passo 2
Precisamos da superfície parametrizada, as antes, quem é mais vantajoso nos perguntarmos quem é a superfície ?
No nosso caso, estamos lidando com a parte do cilindro deslocado, pois...
Completando quadrado:
É um cilindro deslocado em de raio :
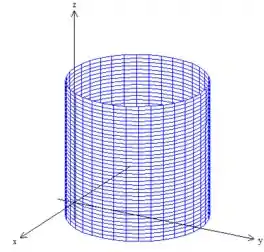
Mas queremos apenas a parte do cilindro que está acima do (palno ) e abaixo do cone:
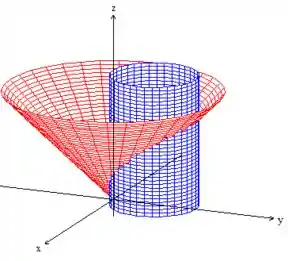
Não se preocupe na hora de fazer um esboço, afinal isso é apenas para nos dar uma noção de quem que estamos trabalhando. O que queremos mesmo é parametrizar isso daí, então bora?
Passo 3
Bem, estamos trabalhando com um pedaço de cilindro, então nada mais justo que utilizar uma parametrização “prima” das coordenadas cilíndricas (lembre-se que o cilindro está deslocado em ):
Agora tome muito cuidado! Uma superfície, mesmo no espaço, tem duas dimensões, certo? Então ela precisa sempre de dois parâmetros para descrevê-la. No nosso caso, é só o ângulo e o próprio , esse desaparece virando o raio do cilindro que estamos trabalhando...
Logo a parametrização é...
Ou, com uma anotação um pouco mais elegante do ponto de vista da matemática...
Passo 4
Ok, agora nos falta a segunda parte do problema que é encontrar o domínio dos parâmetros: onde eles estão variando.
Bem, como a parametrização é prima das coordenadas cilíndricas, o ângulo gira no plano ao redor do eixo do cilindro:
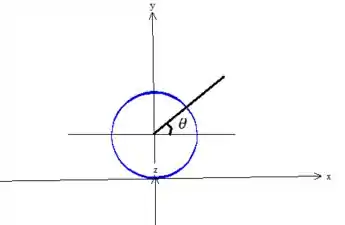
Como pode ver na projeção da superfície no plano , precisamos de um dando uma volta completa:
Passo 5
Enquanto isso, o varia entre o plano e o cone:
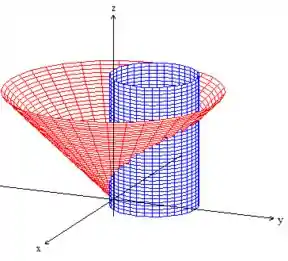
Trocando os termos e pelos parâmetros...
Como ...
Multiplicando o interior por quatro e dividindo ao mesmo tempo...
Lembrando que , então, considerando ...
Extraindo a raiz lembrando que a raiz de alguém ao quadrado é o módulo desse alguém (cuidado com isso)
Sabemos que quando está entre e o cosseno de é positivo...
E quando está entre e , o cosseno de é negativo, então pelo módulo...
Guarde essas duas informações, pois quando formos montar a integral, gerará duas interias diferentes devido essa diferença ;)
Passo 6
Beleza, então com essa primeira etapa já resolvida podemos sair em busca do termo ...
Onde esse vetor normal é dado por...
Não precisa se preocupar com a ordem dessas derivadas parciais, pois o módulo no corrige qualquer sinal de menos ( ). Por falar nisso, calculando essas derivadas parciais...
Substituindo tudo dentro do produto vetorial (um determinante lembrando em que a primeira linha estão os vetores , e ...
Então
Bem, ainda não concluímos o termo , pois ele nos exige o módulo de , então devemos extrair a raiz quadrada...
Passo 7
Voltando para integral de linha que estamos resolvendo...
E substituindo esses termos que determinamos (lembrando que , trocamos por que é a região de variação de e ).
Lembrando que foi dividido em duas partes, a primeira é:
Gerando a integral
a segunda é
Gerando...
A integral sobre será a soma das duas...
Resolvendo a º integral:
E agora a segunda...
Ganhamos no final...