Considere a parte da superfície que fica embaixo da superfície , isto é,
- Determine uma parametrização de , especificando o domínio de definição da parametrização.
- Calcule a área da superfície .
Passo 1
Item 1) vamos começar entendendo melhor a superfície dada no problema, e uma boa maneira de fazer isso é entendendo como ela interage com a superfície que está delimitando.
Analisar uma interação, aqui pra gente, é olhar para a intersecção:
Tipo, a gente sabe que e está delimitada por . Vamos montar um sistema com isso, resolver e ver no que dá.
Substituindo o da primeira na inequação de baixo, dessa forma aqui
E resolvendo esse quadrado da diferença...
Observe que podemos cortar esse e passar esses e para o outro lado da inequação, ficando então
Veja que inequação interessante chagamos! Isso nos indica que estamos trabalhando com uma região com o domínio dentro de um círculo de raio e centro na origem.
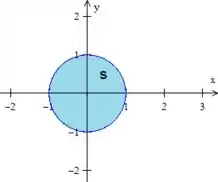
Passo 2
Trabalhando com uma região delimitada da forma acima, nos sugere usar coordenadas cilíndricas né?
E uma equação que é muito interessante para gente aqui também é
Pois bem! a superfície representada por ficará agora sendo representada por
Passo 3
Para a gente encontrar os limites dos nossos parâmetros, vamos olhar bem para o domínio que encontramos
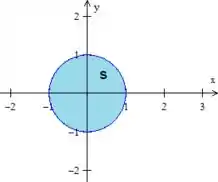
Podemos notar aí que de a , dando uma volta completa e varia de até 1. Se você desconfiar disso, olhe para a equação que delimita o círculo
Notou?! Logo, o domínio dá parametrização é de tal maneira que
Passo 4
Item 2) bem, a gente sabe que área de uma superfície é dada por uma integral de superfície, essa daqui
Resta pra gente encontrar esse que é dada por
Onde o é a norma do vetor normal a superfície e dada pelo produto vetorial das derivadas parciais da parametrização da superfície, ou seja, temos que encontrar isso daqui:
Passo 5
Calculando essas derivadas parciais lembrando que :
E a derivada em relação a :
Indo agora para o produto vetorial desses dois vetores...
Calculando esse determinante
Usando agora o fato de que :
Passo 6
Voltando para o problema, o que realmente queremos é , logo devemos calcular a norma do vetor normal acima. Dessa forma:
Colocando em evidência vamos simplificar isso para
Passo 7
Substituindo na integral de superfície que temos que calcular todos esses ingredientes
Agora a gente usa uma substituição simples:
E os limites vão ficar:
Então:
Resolvendo, finalmente, a integral dupla, teremos
Resposta
Item 1) ; com
Item 2)